CBSE 10th Mathematics | Applications of Quadratic Equations

Applications of Quadratic Equations

Problem:

The sum of two numbers is 15. If the sum of their reciprocals is $\displaystyle \frac{3}{10}$ , find the numbers.

Solution:

Let the required numbers be x and 15 – x. Then,

According to question, we have

$\displaystyle \frac{1}{x}+\frac{1}{15-x}=\frac{3}{10}$

Þ $\displaystyle \frac{15-x+x}{x(15-x)}=\frac{3}{10}$

Þ $\displaystyle \frac{15}{x(15-x)}=\frac{3}{10}$

Þ $\displaystyle 150=3x(15-x)$

Þ 150 = $\displaystyle 45x-3{{x}^{2}}$

Þ $\displaystyle 3{{x}^{2}}-45x+150=0$

or $\displaystyle {{x}^{2}}-15x+50=0$

Þ $\displaystyle {{x}^{2}}-10x-5x+50=0$

Þ $\displaystyle x(x-10)-5(x-10)=0$

Þ $\displaystyle (x-10)(x-5)=0$

Þ $\displaystyle x-10=0$ or $\displaystyle x-5=0$

Þ x = 10 or, x = 5

Hence, the two numbers are 10 and 5.

Problem:

A two-digit number is such that the product of its digits is 14. When 45 is added to this number, the digits interchange their places. Find the number.

Solution:

Let the tens digit be x then the units digit $\displaystyle =\frac{14}{x}$ [ $\displaystyle \because$ product of two digit is 14]

Then, the two digit number is $\displaystyle \left( 10x+\frac{14}{x} \right)$ .

Reverse number = $\displaystyle \left( \frac{140}{x}+x \right)$

According to question, we have

$\displaystyle 10x+\frac{14}{x}+45=\frac{140}{x}+x$

$\displaystyle 10{{x}^{2}}+14+45x=140+{{x}^{2}}$

$\displaystyle 10{{x}^{2}}-{{x}^{2}}+45x+14-140=0$

$\displaystyle 9{{x}^{2}}+45x-126=0$

or $\displaystyle {{x}^{2}}+5x-14=0$

$\displaystyle {{x}^{2}}+7x-2x-14=0$

$\displaystyle x(x+7)-2(x+7)=0$

$\displaystyle (x+7)(x-2)=0$

$\displaystyle x=2$ ; $\displaystyle x=-7$ is rejected as digit can not be negative

\ $\displaystyle x=2$ and other digit $\displaystyle =\frac{14}{2}=7$

Hence, the required number is 10 × 2 + 7 i.e. 27.

Problem:

A two-digit number is 4 times the sum of its digits and twice the product of its digits. Find the number.

Solution:

Let the tens digit be x and the units digit be y.

Since, the two digit number is 4 times the sum of its digits, we have

$\displaystyle 10x+y=4(x+y)$

Þ $\displaystyle 10x+y=4x+4y$

Þ $\displaystyle 6x=3y$

Þ $\displaystyle x=\frac{y}{2}$ …(i)

Since, the two-digit number is twice the product of its digits, we have

$\displaystyle (10x+y)=2(xy)$

Þ $\displaystyle 10x+y-2xy=0$ …(ii)

Substituting $\displaystyle x$ = $\displaystyle \frac{y}{2}$ from equation (i) in equation (ii), we have

$\displaystyle 10\times \frac{y}{2}+y-2\times \frac{y}{2}\times y=0$

Þ $\displaystyle -{{y}^{2}}+5y+y=0$

or $\displaystyle {{y}^{2}}-6y=$ 0 Þ $\displaystyle y(y-6)=0$

Þ Either y = 0 [rejected] or $\displaystyle y-6=0$

Þ $\displaystyle y=6$

\ $\displaystyle x=\frac{6}{2}=3$ [from (i)]

The required number is (10 × 3 + 6) = 36

Problem:

A pole has to be erected at a point on the boundary of a circular park of diameter 13 meters in such a way that the differences of its distances from two diametrically opposite fixed gates Q and R on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?

Solution:

Let P be the required location of the pole. Let the distance of the pole from the gate R be x m, i.e. RP = x m. Now the difference of the distances of the pole from the two gates = QP – RP (or, RP – QP) = 7 m. Therefore, QP = (x + 7) m.

Now, QR = 13m, and since QR is a diameter.

$\displaystyle \angle QPR=90{}^\circ$ (Angle in a semicircle is right angle)

Therefore, $\displaystyle Q{{P}^{2}}+P{{R}^{2}}=Q{{R}^{2}}$ (By Pythagoras theorem)

i.e., $\displaystyle {{(x+7)}^{2}}+{{x}^{2}}={{13}^{2}}$

i.e., $\displaystyle {{x}^{2}}+14x+49+{{x}^{2}}=169$

i.e., $\displaystyle 2{{x}^{2}}+14x-120=0$

So, the distance x of the pole from gate R satisfies the equation

$\displaystyle {{x}^{2}}+7x-60=0$

We will find its discriminant and find whether it would be possible

$\displaystyle {{b}^{2}}-4ac={{7}^{2}}-4\times 1\times (-60)=289$ > 0

So, the given quadratic equation has two real roots, and it is possible to erect the pole on the boundary of the park.

Solving the quadratic equation $\displaystyle {{x}^{2}}+7x-60=0$ , by quadratic formula, we have

$\displaystyle x=\frac{-b\pm \sqrt{D}}{2a}$

$\displaystyle x=\frac{-7\pm \sqrt{289}}{2}=\frac{-7\pm 17}{2}$

Therefore, x = 5 or –12.

Since x is the distance between the pole and the gate R, it must be positive. Therefore, x = –12 is rejected. So, x = 5.

Thus, the pole has to be erected on the boundary of the park at a distance of 5m from the gate R and 12 m from the gate Q.

Problem:

A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs.90, find the number of articles produced and the cost of each article.

Solution:

Let the number of pottery articles, produced on a particular day be x.

Cost of production of each article = Rs.(2x + 3)

\ Total cost of production of x articles = Rs.(2x + 3) × x … (i)

It is given that the total cost of production = Rs.90 …(ii)

\ $\displaystyle (2x+3)x=90$

Þ $\displaystyle 2{{x}^{2}}+3x-90=0$

Þ $\displaystyle 2{{x}^{2}}-12x+15x-90=0$

Þ $\displaystyle 2x(x-6)+15(x-6)=0$

Þ $\displaystyle (x-6)(2x+15)=0$

Þ x = 6 or $\displaystyle x=-\frac{15}{2}$ (rejected as the cost cannot be negative)

\ $\displaystyle x=6$

Hence number of articles produced in a day = 6

Cost of production of each article = Rs. (2 ´ 6 + 3)

= Rs. 15

Problem:

X and Y are centres of two circles of radii 9 cm and 2 cm respectively and XY = 17cm. Z is the centre of a circle of radius r cm. which touches the above circles externally. Given that ÐXZY = 90°, write an equation in r and solve it for r.

Solution:

According to question, we have

$\displaystyle {{(r+2)}^{2}}+{{(r+9)}^{2}}={{17}^{2}}$ [By Pythagoras theorem]

Þ $\displaystyle {{r}^{2}}+4r+4+{{r}^{2}}+18r+81=289$

Þ $\displaystyle 2{{r}^{2}}+22r-204=0$

or $\displaystyle {{r}^{2}}+11r-102=0$ [Required equation]

Þ $\displaystyle {{r}^{2}}+17r-6r-102=0$

Þ $\displaystyle r(r+17)-6(r+17)=0$

Þ $\displaystyle (r+17)(r-6)=0$

Þ $\displaystyle r=-17$ or r = 6 cm

As r can not be negative \ r = –17 is rejected

Hence r = 6 cm

Problem:

A farmer wishes to grow a 100 m2 rectangular vegetable garden. Since he has with him only 30m barbed wire, he fences three sides of the rectangular garden letting compound wall of his house act as the fourth side-fence. Find the dimensions of his garden.

Solution:

Let length of one side of rectangle = (x) m

Total length of wire = 30 m

Then, the length of adjacent side = (30 – 2x) m

\ Area = x (30 – 2x) = 30x – 2×2

By the given condition,

$\displaystyle 30x-2{{x}^{2}}=100$

$\displaystyle 2{{x}^{2}}-30x+100=0$

or $\displaystyle {{x}^{2}}-15x+50=0$

Þ $\displaystyle {{x}^{2}}-10x-5x+50=0$

Þ $\displaystyle x(x-10)-5(x-10)=0$

Þ $\displaystyle (x-5)(x-10)=0$

Þ $\displaystyle x-5=0$

or $\displaystyle x-10=0$

Þ $\displaystyle x=5$

or x = 10

Case 1: If one side = 10 m, then 2nd side = 30 – 2 × 10 = 30 – 20 = 10 m

Case 2: If one side = 5 m, then 2nd side = 30 – 2 × 5 = 30 – 10 = 20 m

So, the dimensions of garden are either 10 m × 10 m or 20 m × 5 m.

Problem:

A piece of cloth cost Rs.200. If the piece was 5m longer and each metre of cloth costs Rs.2 less, the cost of the piece would have remained unchanged. How long is the piece and what is its original rate per metre?

Solution:

Let the length of the piece be x metres.

Cost of the cloth	Rs.200	Rs.200
Length of the piece	x metres	(x + 5) metres
Rate per metre	Rs. $\displaystyle \frac{200}{x}$	Rs. $\displaystyle \frac{200}{x+5}$

If the piece is 5 m longer then rate per metre is Rs.2 less.

\ $\displaystyle \frac{200}{x}-\frac{200}{x+5}=2$

Þ $\displaystyle 200\left[ \frac{x+5-x}{x(x+5)} \right]=2$

Þ $\displaystyle 200\left[ \frac{5}{{{x}^{2}}+5x} \right]=2$

Þ $\displaystyle {{x}^{2}}+5x=500$

Þ $\displaystyle {{x}^{2}}+5x-500=0$

Þ $\displaystyle {{x}^{2}}+25x-20x-500=0$

Þ $\displaystyle x(x+25)-20(x+25)=0$

Þ $\displaystyle (x+25)(x-20)=0$

Þ $\displaystyle x+25=0$ or $\displaystyle x-20=0$

Þ $\displaystyle x=-25$ (rejected, as length cannot be negative) or x = 20

Rate per metre = Rs. $\displaystyle \frac{200}{x}=Rs.\,\frac{200}{20}=$ Rs.10

Hence, the length of the piece of cloth is 20 metres and the rate per metre is Rs.10

Problem:

The sum of squares of two positive integers is 208. If the square of the larger number is 18 times the smaller number. Find the numbers.

Solution:

Let x be the smaller number. Then the square of the larger number will be 18x. Since the sum of the squares of these two positive integers is 208. We have

$\displaystyle {{x}^{2}}+18x=208$

Þ $\displaystyle {{x}^{2}}+26x-8x-208=0$

Þ $\displaystyle x(x+26)-8(x+26)=0$

Þ $\displaystyle (x-8)(x+26)$ = 0

Þ $\displaystyle x-8=0$ or $\displaystyle x+26=0$

Þ $\displaystyle x=8$ or –26

Since the numbers are positive, x = –26 is rejected

\ x = 8 and square of the larger positive integer = 18 × 8 = 144

\ Larger number = $\displaystyle \sqrt{144}=12$

Hence, the larger number is 12 and the smaller number is 8.

Problem:

The denominator of a fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is 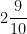$\displaystyle 2\frac{9}{10}$ , find the fraction.

Solution:

Let the numerator of the fraction be x.

Then, the denominator = 2x + 1. Fraction = $\displaystyle \frac{x}{2x+1}$

According to question, we have

$\displaystyle \frac{x}{2x+1}+\frac{2x+1}{x}=\frac{29}{10}$

Þ $\displaystyle \frac{{{x}^{2}}+{{(2x+1)}^{2}}}{x(2x+1)}=\frac{29}{10}$

Þ $\displaystyle \frac{{{x}^{2}}+4{{x}^{2}}+4x+1}{2{{x}^{2}}+x}=\frac{29}{10}$

Þ $\displaystyle \frac{5{{x}^{2}}+4x+1}{2{{x}^{2}}+x}=\frac{29}{10}$

Þ $\displaystyle 50{{x}^{2}}+40x+10=58{{x}^{2}}+29x$

Þ $\displaystyle 8{{x}^{2}}-11x-10=0$

Þ $\displaystyle x=\frac{11\pm \sqrt{121+320}}{16}=\frac{11\pm \sqrt{441}}{16}=\frac{11\pm 21}{6}$

Þ $\displaystyle x=\frac{32}{16}$ or $\displaystyle -\frac{10}{16}$

Þ $\displaystyle x=2$ or $\displaystyle \frac{-5}{8}$ [Rejected]

Denominator = 2x + 1 = 2(2) + 1 = 5

Hence, the required fraction is $\displaystyle \frac{2}{5}$ .

Problem:

Out of a group of swans, $\displaystyle \frac{7}{2}$ times the square root of the number are playing on the shore of a tank. The two remaining ones are playing, with amorous fight, in the water. What is the total number of swans?

Solution:

Let the total number of swans be x. Then,

Number of swans playing on the shore of the tank = $\displaystyle \frac{7}{2}\sqrt{x}$

It is given that there are two remaining swans.

\ $\displaystyle x=\frac{7}{2}\sqrt{x}+2$

Þ $\displaystyle x-\frac{7}{2}\sqrt{x}-2=0$

Put $\displaystyle \sqrt{x}=y\,\ \ \ \ \Rightarrow \ \ \ \ x={{y}^{2}}$

Þ $\displaystyle {{y}^{2}}-\frac{7}{2}y-2=0$

Þ $\displaystyle 2{{y}^{2}}-7y-4=0$

Þ $\displaystyle 2{{y}^{2}}-8y+y-4=0$

Þ $\displaystyle 2y(y-4)+1(y-4)=0$

Þ $\displaystyle (y-4)(2y+1)=0$

Þ $\displaystyle y=4$ or, $\displaystyle y=-\frac{1}{2}$

Þ $\displaystyle y=4$ [Q y = –1/2 is not possible]

Þ $\displaystyle x={{y}^{2}}={{4}^{2}}=1$ 6

Hence, the total number of swans is 16.

Problem:

A plane left 30 minutes later than the schedule time and in order to reach its destination 1500 km away in time it has to increase its speed by 250 km/hr from its usual speed. Find its usual speed.

Solution:

Let the usual speed of the plane be x km/hr. Then,

Time taken to cover 1500 km with the usual speed = $\displaystyle \frac{1500}{x}$ hrs.

Time taken to cover 1500 km with the increased speed of

$\displaystyle (x+250)$ km/hr = $\displaystyle \frac{1500}{x+250}$

According to question

\ $\displaystyle \frac{1500}{x}=\frac{1500}{x+250}+\frac{1}{2}$ [30 minutes = $\displaystyle \frac{30}{60}$ hr = $\displaystyle \frac{1}{2}$ hr]

Þ $\displaystyle \frac{1500}{x}-\frac{1500}{x+250}=\frac{1}{2}$

Þ $\displaystyle \frac{1500x+1500\times 250-1500x}{x(x+250)}=\frac{1}{2}$

Þ $\displaystyle \frac{1500\times 250}{{{x}^{2}}+250x}=\frac{1}{2}$

Þ $\displaystyle 750000={{x}^{2}}+250x$

Þ $\displaystyle {{x}^{2}}+250x-750000=0$

Þ $\displaystyle {{x}^{2}}+1000x-750x-750000=0$

Þ $\displaystyle x(x+1000)-750(x+1000)=0$

Þ $\displaystyle (x+1000)(x-750)=0$

Þ x = – 1000 or $\displaystyle x=750$

Þ $\displaystyle x=750$ [Q speed cannot be negative]

Hence, the usual speed of the plane is 750 km/hr.

Problem:

Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km/hr faster than the second train. If after two hours, they are 50 km apart, find the average speed of each train.

Solution:

Let the speed of the second train be x km/hr. Then, the speed of the first train is $\displaystyle (x+5)$ km/hr.

Let O be the position of the railway station from which the two trains leave.

Distance traveled by the first train in 2 hours = OA = Speed × Time

= 2(x + 5) km

Distance traveled by the second train in 2 hours = OB = 2x km

In DOAB by using Pythagoras theorem, we have

$\displaystyle A{{B}^{2}}=O{{A}^{2}}+O{{B}^{2}}$

Þ $\displaystyle {{50}^{2}}={{\{2(x+5)\}}^{2}}+{{(2x)}^{2}}$

Þ 2500 = $\displaystyle 4{{(x+5)}^{2}}+4{{x}^{2}}$

Þ $\displaystyle 2500=4({{x}^{2}}+25+10x)+4{{x}^{2}}$

Þ $\displaystyle 8{{x}^{2}}+40x-2400=0$

or $\displaystyle {{x}^{2}}+5x-300=$ 0

Þ $\displaystyle {{x}^{2}}+20x-15x-300=0$

Þ $\displaystyle x(x+20)-15(x+20)=0$

Þ $\displaystyle (x+20)(x-15)=0$

Þ $\displaystyle x=-20$ or, x = 15

Þ x = 15

Hence, the speed of the second train is 15 km/hr and, the speed of the first train is 20km/hr.

Problem:

The hypotenuse of a right triangle is 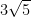$\displaystyle 3\sqrt{5}$ cm. If the smaller side is tripled and the larger side is doubled, the new hypotenuse will be 15cm. Find the length of each side.

Solution:

Let the smaller side of the right triangle be x cm and the larger side by y cm. Then,

$\displaystyle {{x}^{2}}+{{y}^{2}}={{(3\sqrt{5})}^{2}}$ [Using Pythagoras Theorem]

Þ $\displaystyle {{x}^{2}}+{{y}^{2}}=45$ …(i)

If the smaller side is tripled and the larger side be doubled, the new hypotenuse is 15 cm.

\ $\displaystyle {{(3x)}^{2}}+{{(2y)}^{2}}={{15}^{2}}$

Þ $\displaystyle 9{{x}^{2}}+4{{y}^{2}}=225$

From equation (i), we get $\displaystyle {{y}^{2}}=45-{{x}^{2}}$

Putting $\displaystyle {{y}^{2}}=45-{{x}^{2}}$ in equation (ii), we get

$\displaystyle 9{{x}^{2}}+4(45-{{x}^{2}})=225$

Þ $\displaystyle 5{{x}^{2}}+180=225$

Þ $\displaystyle 5{{x}^{2}}=45$ Þ $\displaystyle {{x}^{2}}=9$ Þ x = ±3

But, length of a side cannot be negative. Therefore, x= 3.

Putting x = 3 in (i), we get

$\displaystyle 9+{{y}^{2}}=45$ Þ $\displaystyle {{y}^{2}}=36$ Þ y = 6

Hence, the length of the smaller side is 3 cm and the length of the larger side is 6cm.

Problem:

A takes 6 days less than the time taken by B to finish a piece of work. If both A and B together can finish it in 4 days, find the time taken by B to finish the work.

Solution:

Suppose B alone takes x days to finish the work. Then, A alone can finish it in (x–6) days.

In x days B finishes = 1 work

\ In one day B will finish $\displaystyle =\frac{1}{x}$ work

In (x – 6) days A finishes = 1 work

\ In one day A will finish $\displaystyle =\frac{1}{x-6}$ work

\ (A¢s one day’s work) + (B¢s one day’s work) = $\displaystyle \frac{1}{x}+\frac{1}{x-6}$

According to question $\displaystyle (A+B)\prime s$ one day’s work = $\displaystyle \frac{1}{4}$ \ we have

Þ $\displaystyle \frac{1}{x}+\frac{1}{x-6}=\frac{1}{4}$

Þ $\displaystyle \frac{x-6+x}{x(x-6)}=\frac{1}{4}$ Þ $\displaystyle \frac{2x-6}{{{x}^{2}}-6x}=\frac{1}{4}$

Þ $\displaystyle 8x-24={{x}^{2}}-6x$

Þ $\displaystyle {{x}^{2}}-14x+24=0$

Þ $\displaystyle {{x}^{2}}-12x-2x+24=0$

Þ $\displaystyle (x-12)(x-2)=0$

Þ x = 12 or, x = 2

But, x cannot be less than 6. So, x = 12.

Hence, B along can finish the work in 12 days.

Problem:

A swimming pool is filled with three pipes with uniform flow. The first two pipes operating simultaneously fill the pool in the same time during which the pool is filled by the third pipe alone. The second pipe fills the pool five hours faster than the first pipe and four hours slower than the third pipe. Find the time required by each pipe to fill the pool separately.

Solution:

Let x be the number of hours required by the second pipe along to fill the pool. Then, the first pipe takes (x + 5) hours. While the third pipe takes (x – 4) hours to fill the pool.

In $\displaystyle (x+5)$ hours first pipe fills = 1 tank

In 1 hour first pipe will fill = $\displaystyle \frac{1}{x+5}$ tank

Similarly in 1 hour second pipe will fill = $\displaystyle \frac{1}{x}$ tank

In 1 hour third pipe will fill = $\displaystyle \frac{1}{x-4}$ tank

According to question, we have

Þ $\displaystyle \frac{1}{x+5}+\frac{1}{x}=\frac{1}{x-4}$ Þ $\displaystyle \frac{x+x+5}{{{x}^{2}}+5x}=\frac{1}{x-4}$

Þ $\displaystyle (2x+5)(x-4)={{x}^{2}}+5x$

Þ $\displaystyle {{x}^{2}}-8x-20=0$

Þ $\displaystyle {{x}^{2}}-10x+2x-20=0$

Þ $\displaystyle x(x-10)+2(x-10)$ = 0

Þ $\displaystyle (x-10)(x+2)=0$

Þ x = 10 or, x = –2

But, x cannot be negative. So, x = 10.

Hence, the timings required by first, second and third pipes to fill the pool individually are 15 hours, 10 hours and 6 hours respectively.

Problem:

There is a square field whose side is 44 m. A square flower bed is prepared in its centre leaving a gravel path all round the flower bed. The total cost of laying the flower bed and gravelling the path at Rs.2.75 and Rs.1.50 per square metre, respectively, is Rs.4904. Find the width of the gravel path.

Solution:

Let the width of the gravel path be x metres. Then,

Each side of the square flower bed (PQRS) = (44 – 2x) metres.

Now, area of the square field (ABCD)

= 44 × 44 = 1936 m²

Area of the flower bed = $\displaystyle {{(44-2x)}^{2}}$ m2

\ Area of the gravel path

= Area of the field (ABCD) – Area of the flower bed (PQRS)

= 1936 – (44 – 2x)²

= 1936 – (1936 – 176x + 4×2)

= (176x – 4×2) m²

Cost of laying the flower bed = (Area of the flower bed) (Rate per sq. m)

= $\displaystyle {{(44-2x)}^{2}}\times \frac{275}{100}=\frac{11}{4}{{(44-2x)}^{2}}=11\,{{(22-x)}^{2}}$

Cost of gravelling the path = Area of the path × Rate per sq. m

= $\displaystyle (176x-4{{x}^{2}})\frac{150}{100}=6(44x-{{x}^{2}})$

It is given that the total cost of laying the flower bed and gravelling the path is Rs.4904.

\ $\displaystyle 11{{(22-x)}^{2}}+6(44x-{{x}^{2}})=4904$

Þ $\displaystyle 11(484-44x+{{x}^{2}})+(264x-6{{x}^{2}})=4904$

Þ $\displaystyle 5{{x}^{2}}-220x+5324=4904$

Þ $\displaystyle 5{{x}^{2}}-220x+420=0$

or $\displaystyle {{x}^{2}}-44x+84=0$

Þ $\displaystyle {{x}^{2}}-42x-2x+84=0$

Þ $\displaystyle x(x-42)-2(x-42)=0$

Þ $\displaystyle (x-2)(x-42)=0$

Þ x = 2 or, x = 42

But, x ¹ 42, as the side of the square is 44 m. Therefore, x = 2.

Hence, the width of the gravel path is 2 metres.

CBSE 10th Mathematics | Applications of Quadratic Equations

Applications of Quadratic Equations

Problem:

The sum of two numbers is 15. If the sum of their reciprocals is , find the numbers.

Solution:

Problem:

A two-digit number is such that the product of its digits is 14. When 45 is added to this number, the digits interchange their places. Find the number.

Solution:

Problem:

A two-digit number is 4 times the sum of its digits and twice the product of its digits. Find the number.

Solution:

Problem:

Solution:

Problem:

Solution:

Problem:

X and Y are centres of two circles of radii 9 cm and 2 cm respectively and XY = 17cm. Z is the centre of a circle of radius r cm. which touches the above circles externally. Given that ÐXZY = 90°, write an equation in r and solve it for r.

Solution:

Problem:

A farmer wishes to grow a 100 m2 rectangular vegetable garden. Since he has with him only 30m barbed wire, he fences three sides of the rectangular garden letting compound wall of his house act as the fourth side-fence. Find the dimensions of his garden.

Solution:

Problem:

A piece of cloth cost Rs.200. If the piece was 5m longer and each metre of cloth costs Rs.2 less, the cost of the piece would have remained unchanged. How long is the piece and what is its original rate per metre?

Solution:

Problem:

The sum of squares of two positive integers is 208. If the square of the larger number is 18 times the smaller number. Find the numbers.

Solution:

Problem:

The denominator of a fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is , find the fraction.

Solution:

Problem:

Out of a group of swans, times the square root of the number are playing on the shore of a tank. The two remaining ones are playing, with amorous fight, in the water. What is the total number of swans?

Solution:

Problem:

A plane left 30 minutes later than the schedule time and in order to reach its destination 1500 km away in time it has to increase its speed by 250 km/hr from its usual speed. Find its usual speed.

Solution:

Problem:

Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km/hr faster than the second train. If after two hours, they are 50 km apart, find the average speed of each train.

Solution:

Problem:

The hypotenuse of a right triangle is cm. If the smaller side is tripled and the larger side is doubled, the new hypotenuse will be 15cm. Find the length of each side.

Solution:

Problem:

A takes 6 days less than the time taken by B to finish a piece of work. If both A and B together can finish it in 4 days, find the time taken by B to finish the work.

Solution:

Problem:

Solution:

Problem:

Solution:

Share this:

Like this:

The sum of two numbers is 15. If the sum of their reciprocals is $\displaystyle \frac{3}{10}$ , find the numbers.

The denominator of a fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is $\displaystyle 2\frac{9}{10}$ , find the fraction.

Out of a group of swans, $\displaystyle \frac{7}{2}$ times the square root of the number are playing on the shore of a tank. The two remaining ones are playing, with amorous fight, in the water. What is the total number of swans?

The hypotenuse of a right triangle is $\displaystyle 3\sqrt{5}$ cm. If the smaller side is tripled and the larger side is doubled, the new hypotenuse will be 15cm. Find the length of each side.