CBSE 10th Mathematics | Arithmetic Progressions | nth Term of an Arithmetic Progression

nth Term of an Arithmetic Progression

Let $\displaystyle {{a}_{1}},{{a}_{2}},{{a}_{3}}$ …….. be an A.P., with first term as a, and common difference as d.

First term is = a (i)

Second term $\displaystyle ({{a}_{2}})$ = a + d (ii)

= $\displaystyle a+(2-1)d$

Third term $\displaystyle ({{a}_{3}})$ = $\displaystyle {{a}_{2}}+d$ (iii)

= $\displaystyle a+d+d$ [from (i)]

= $\displaystyle a+2d$

or = $\displaystyle a+(3-1)d$

Fourth term $\displaystyle {{a}_{4}}={{a}_{3}}+d$

or = $\displaystyle a+2d+d$ [from (iii)]

= $\displaystyle a+3d$

= $\displaystyle a+(4-1)d$

\ nth term a_n $\displaystyle =a+(n-1)d$

Note: The nth term of the A.P. with first term a & common difference d is given by $\displaystyle {{a}_{n}}=a+(n-1)d$

$\displaystyle {{a}_{n}}$ is also called as general term of an A.P.

If there are P terms in the A.P. then a_p represents the last term which can also be denoted by l.

Problems based on nth TERM OF AN Arithmetic Progression

Problem:

Find the 18^th term and n^th term for the sequence 7, 4, 1, –2, –5.

Solution:

Here a = 7

and d = $\displaystyle {{a}_{2}}-{{a}_{1}}$

= 4 – 7 = – 3

n = 18

$\displaystyle {{a}_{n}}=a+\left( n-1 \right)d$

$\displaystyle {{a}_{18}}=7+\left( 18-1 \right)\times -3$

= 7 + 17 ´ –3

= 7 – 51

= –44

$\displaystyle {{a}_{n}}=a+\left( n-1 \right)d$

= 7 + (n – 1) (–3)

= 7 – 3n + 3

= 10 – 3n

Problem:

Which term of the A.P. 7, 12, 17, ….. is 87?

Solution:

a = 7

$\displaystyle d={{a}_{2}}-{{a}_{1}}$

= 12 – 7 = 5

$\displaystyle {{a}_{n}}=87$

As $\displaystyle {{a}_{n}}=a+\left( n-1 \right)d$

87 = 7 + (n – 1) ´ 5

$\displaystyle 87-7=5n-5$

$\displaystyle 80+5=5n$

$\displaystyle \frac{85}{5}=n$

17 = n

\ 17^th term of give A.P. is 87

Problem:

How many terms are there in A.P. 7, 13, 19, …….., 205.

Solution:

a = 7

$\displaystyle d={{a}_{2}}-{{a}_{1}}$

= 13 – 7 = 6

$\displaystyle {{a}_{n}}=a+\left( n-1 \right)d$

$\displaystyle 205=7+\left( n-1 \right)\times 6$

205 – 7 = 6n– 6

198 + 6 = 6n

$\displaystyle \frac{204}{6}=n$ or 34 = n

\ Given A.P. has 34 terms

Problem:

Check whether –150 is term of the A.P. 11, 8, 5, 2, …….?

Solution:

a = 11

$\displaystyle d={{a}_{2}}-{{a}_{1}}$

= 8 – 11 = -3

let $\displaystyle {{a}_{n}}=-150$ [Assume]

$\displaystyle -150-11=-3n+3$

$\displaystyle -161-3=-3n$

$\displaystyle -164=-3n$

$\displaystyle \frac{164}{3}=n$

As number of term can’t be in fraction, \ –150 is not a term of the given A.P.

Problem:

In the following A.P. find the missing terms in the boxes.

(i) 5, , , $\displaystyle 9\frac{1}{2}$ (ii) –4, , , , , 6

Solution:

(i) Here a = 5

& $\displaystyle {{a}_{4}}=9\frac{1}{2}$ or $\displaystyle \frac{19}{2}$

Now, $\displaystyle {{a}_{4}}=a+3d$

$\displaystyle \frac{19}{2}=5+3d$

$\displaystyle \frac{19}{2}-5=3d$

$\displaystyle \frac{9}{2}=3d$

$\displaystyle \frac{9}{6}=d$

\ $\displaystyle d=\frac{3}{2}$

\ $\displaystyle {{a}_{2}}=a+d=5+\frac{3}{2}=\frac{13}{2}$

$\displaystyle {{a}_{3}}={{a}_{2}}+d=\frac{13}{2}+\frac{3}{2}=\frac{16}{2}=8$

Hence

(ii) Here $\displaystyle a=-4$

$\displaystyle {{a}_{6}}=6$

As $\displaystyle {{a}_{6}}=a+5d$

6 = –4 + 5d

$\displaystyle \frac{10}{5}=d$

d = 2

\ $\displaystyle {{a}_{2}}=a+d=-4+2=-2$

$\displaystyle {{a}_{3}}={{a}_{2}}+d=-2+2=0$

$\displaystyle {{a}_{4}}={{a}_{3}}+d=0+2=2$

$\displaystyle {{a}_{5}}={{a}_{4}}+d=2+2=4$

Problem:

For what value of n, the nth terms of A.P’s 63, 65, 67, ……… and 3, 10, 17, …… are equal.

Solution:

First sequence is 63, 65, 67, ……..

a = 63

d₁ = 65 – 63 = 2

$\displaystyle {{a}_{n}}=63+\left( n-1 \right)2$

= 63 + 2n–2

= 61 + 2n

Second sequence is 3, 10, 17, ………..

\ $\displaystyle b=3,\,\,\,{{d}_{2}}=7$

\ $\displaystyle {{b}_{n}}=3+\left( n-1 \right)7$

= $\displaystyle 3+7n-7$

= 7n–4

According to question

61 + 2n = 7n– 4

61 + 4 = 7n– 2n

65 = 5n

$\displaystyle \frac{65}{5}=n$

\n = 13

Problem:

Two A.P.s have the same common difference. If the difference between their 100^th terms is 100, what is the difference between their 1000^th terms?

Solution:

Let the common difference of two A.P.s be d

Then, their 100^th terms will be

$\displaystyle {{a}_{100}}={{a}_{1}}+99d;\,\,\,\,\,{{b}_{100}}={{b}_{1}}+99d$

According to question $\displaystyle {{a}_{100}}-{{b}_{100}}=100$

i.e. …(i)

Now, difference between their 1000^th terms

$\displaystyle ={{a}_{1000}}-{{b}_{1000}}=\left( {{a}_{1}}+999d \right)-\left( {{b}_{1}}+999d \right)$

$\displaystyle ={{a}_{1}}-{{b}_{1}}=100$ [By equation (i)]

Problem:

Which term of the arithmetic progression 3, 10, 17, …. will be 84 more than its 13^th term?

Solution:

The give A.P. is 3, 10, 17, ……

Here, a (first term) = 3

d (common difference)= 10 – 3 = 7

$\displaystyle {{a}_{n}}=a+\left( n-1 \right)d$

$\displaystyle {{a}_{13}}=3+(13-1)7$

= 3 + 12 ´ 7 = 3 + 84 = 87

Let n^th term be 84 more than the 13^th term of the given A.P.

So, we get $\displaystyle {{a}_{n}}=84+{{a}_{13}}$

$\displaystyle a+\left( n-1 \right)d=84+a+12d$

$\displaystyle d\left( n-1-12 \right)=84$

$\displaystyle 7\left( n-13 \right)=84$

$\displaystyle n-13=\frac{84}{7}=12$

$\displaystyle n=12+13=25$

\ The 25^th term of the given A.P. will be 84 more than its 13^th term.

Problem:

Find the 31^st term of an A.P. whose 11^th term is 38 and the 16^th term is 73.

Solution:

Let a be the 1^st term and d the common difference.

Here $\displaystyle {{a}_{11}}=a+10d=38$ …(i)

$\displaystyle {{a}_{16}}=a+15d=73$ …(ii)

Subtracting (ii) and (i), we get

$\displaystyle a+10d-a-15d=38-73$

Putting d = 7 in (i), we get

$\displaystyle a+10\times 7=38$

$\displaystyle a=38-70=-32$

\ $\displaystyle {{a}_{31}}=a+30d=-32+30\times 7=-32+210=178$

Hence, 31^st term is 178.

Problem:

How many three digit numbers are divisible by 7?

Solution:

Three digit numbers which are divisible by 7 are 105, 112, 119, …, 994.

Here, $\displaystyle a=105,\,\,\,\,\,d=7,\,\,\,\,\,{{a}_{n}}=994$

\ $\displaystyle a+(n-1)d=994$

$\displaystyle 105+(n-1)7=994$

Þ $\displaystyle 7(n-1)=994-105=889$

Þ $\displaystyle n-1=\frac{889}{7}$

Þ n – 1 = 127

n = 127 + 1 = 128.

\ There are 128 three digit numbers which are divisible by 7

Problem:

A sum of Rs 1000 is invested at 8% simple interest per year. Calculate the interest at the end of each year. Do these interests from an AP? If so, find the interest at the end of 30 years.

Solution:

We know that the formula to calculate simple interest is given by

Simple Interest = $\displaystyle \frac{P\times R\times T}{100}$

So, the interest at the end of the 1^st year = Rs $\displaystyle \frac{1000\times 8\times 1}{100}$ = Rs 80

The interest at the end of the 2^nd year = Rs $\displaystyle \frac{1000\times 8\times 2}{100}$ = Rs 160

The interest at the end of the 3^rd year = Rs $\displaystyle \frac{1000\times 8\times 3}{100}$ = Rs 240

Similarly, we can obtain the interest at the end of the 4^th year, 5^th year, and so on.

So, the interest (in Rs) at the end of the 1^st, 2^nd, 3^rd, ….. years, respectively are 80, 160, 240, …

It is an AP as the difference between the consecutive terns in the list is 80, i.e., d = 80. Also, a = 80.

So, to find the interest at the end of 30 years, we shall find $\displaystyle {{a}_{30}}$ .

Now, $\displaystyle {{a}_{30}}=a+(30-1)d=80+29\times 80=2400$

So, the interest at the end of 30 years will be Rs 2400.

TO FIND nth TERM FROM THE END OF AN A.P.

Consider the following A.P. $\displaystyle a,a+d,\,a+2d,....\left( l-2d \right),\left( l-d \right)$ , $\displaystyle l$

where l is the last term

last term $\displaystyle l$ = $\displaystyle l$ – (1 – 1)d

2^nd last term $\displaystyle l$ –
d = $\displaystyle l$ – (2 – 1) d

3^rd last term $\displaystyle l$ – 2d = $\displaystyle l$ – (3 – 1)d

……………………………

Note: nth term from the end = $\displaystyle l$ – (n – 1) d

Problem:

Find the 5^th term from the end of the AP, 17, 14, 11, ….., –40

Solution:

1^st method

$\displaystyle l=-40,d=14-17=-3$

Using $\displaystyle l-(n-1)d$

5^th term from the end will be

$\displaystyle =-40-(5-1)\times -3$

$\displaystyle =-40-4\times -3$

$\displaystyle =-40+12$

= –28

2^nd method

Sequence can be written as –40, –37, ….11, 14, 17

\ $\displaystyle a=-40$

$\displaystyle d=-37-(-40)$

=–37 + 40

= 3

n = 5

Using $\displaystyle {{a}_{n}}=a+(n-1)d$

= $\displaystyle -40+(5-1)\times 3$

$\displaystyle =-40+4\times 3$

= –40 + 12

= –28

Problem:

The sum of the 4^th and 8^th terms of an A.P. is 24 and sum of 6^th & 10^th terms is 44. Find the first three term of the AP.

Solution:

Using 1^st condition

\ $\displaystyle {{a}_{4}}+{{a}_{8}}=24$

$\displaystyle a+3d+a+7d=24$

$\displaystyle 2a+10d=24$

or $\displaystyle a+5d=12$ …(i)

Using 2^nd condition

$\displaystyle {{a}_{6}}+{{a}_{10}}=44$

or $\displaystyle a+5d+a+9d=44$

$\displaystyle 2a+14d=44$

or $\displaystyle a+7d=22$ …(ii)

Subtracting equation (i) from (ii) we have

$\displaystyle 2d=10$

or d = 5

Putting value of d in equations (i)

$\displaystyle a+5\times 5=12$

$\displaystyle a=12-25$

$\displaystyle a=-13$

\ $\displaystyle {{a}_{2}}=a+d$

$\displaystyle =-13+5=-8$

$\displaystyle {{a}_{3}}=a+2d$

$\displaystyle =-13+2\times 5$

$\displaystyle =-13+10=-3$

Problem:

If the pth term of an A.P. is q and the qth term is p, prove that its nth term is 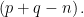$\displaystyle \left( p+q-n \right).$

Solution:

Let a be the first term and d be the common difference of the given A.P.

Then, pth term = q Þ $\displaystyle a+\left( p-1 \right)d=q$ …(i)

qth term = p Þ $\displaystyle a+\left( q-1 \right)d=p$ …(ii)

Subtracting equation (ii) from equation (i), we get

…(iii)

Putting $\displaystyle d=-1$ in equation (i), we get

$\displaystyle a+1-p=q$

\ nth term $\displaystyle =a+\left( n-1 \right)d$

$\displaystyle =\left( p+q-1 \right)+\left( n-1 \right)\times (-1)$ [from equation (iii)]

$\displaystyle =\left( p+q-n \right)$

Problem:

If m times the mth term of an A.P. is equal to n times its nth term, show that the (m + n) term of the A.P. is zero.

Solution:

Let a be the first term and d be the common difference of the given A.P.

According to question, m times the mth term = n times the nth term

Þ $\displaystyle m{{a}_{m}}=n{{a}_{n}}$

Þ $\displaystyle m\left\{ a+\left( m-1 \right)d \right\}=n\left\{ a+\left( n-1 \right)d \right\}$

Þ $\displaystyle m\left\{ a+\left( m-1 \right)d \right\}-n\left\{ a+\left( n-1 \right)d \right\}=0$

Þ $\displaystyle a\left( m-n \right)+\left\{ m\left( m-1 \right)-n\left( n-1 \right) \right\}d=0$

Þ $\displaystyle a\left( m-n \right)+\left( {{m}^{2}}-{{n}^{2}}-m+n \right)d=0$

Þ $\displaystyle a\left( m-n \right)+\left[ \left( m-n \right)\left( m+n \right)-\left( m-n \right) \right]d=0$

Þ $\displaystyle a\left( m-n \right)+\left[ \left( m-n \right)\left( m+n-1 \right)d \right]=0$

Þ $\displaystyle \left( m-n \right)\left[ a+\left( m+n-1 \right)d \right]=0$

Þ $\displaystyle a+\left( m+n-1 \right)d=0$ [ $\displaystyle \because m\ne n$ ]

Þ $\displaystyle {{a}_{m+n}}=0$

\ $\displaystyle \left( m+n \right)$ th term of A.P. is zero

CONDITION FOR TERMS TO BE IN A.P.

If three numbers a, b, c, in order are in A.P. Then,

$\displaystyle b-a=$ common difference = $\displaystyle c-b$

Þ $\displaystyle b-a=c-b$

Þ $\displaystyle 2b=a+c$

Note: a, b, c are in A.P. iff $\displaystyle 2b=a+c$

Problem:

If $\displaystyle 2x,x+10,3x+2$ are in A.P., find the value of x.

Solution:

Since, $\displaystyle 2x,x+10,3x+2$ are in A.P.

\ $\displaystyle 2\left( x+10 \right)=2x+\left( 3x+2 \right)$

Þ $\displaystyle 2x+20=5x+2$

Þ $\displaystyle 3x=18$

Þ x = 6

Problem:

If the numbers a, b, c, d, e form an A.P., then find the value of 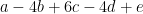$\displaystyle a-4b+6c-4d+e$ .

Solution:

Let D be the common difference of the given A.P. Then,

$\displaystyle b=a+D,c=a+2D,d=a+3D$ and $\displaystyle e=a+4D$

\ $\displaystyle a-4b+6c-4d+e=a-4(a+D)+6(a+2D)-4(a+3D)+(a+4D)$

Þ $\displaystyle a-4b+6c-4d+e=a-4a-4D+6a+12D-4a-12D+a+4D$

Þ $\displaystyle a-4b+6c-4d+e=a-4a+6a-4a+a-4D+12D-12D+4D$

Þ $\displaystyle a-4b+6c-4d+e=0$

CBSE 10th Mathematics | Arithmetic Progressions | nth Term of an Arithmetic Progression

nth Term of an Arithmetic Progression

Problems based on nth TERM OF AN Arithmetic Progression

Problem:

Find the 18th term and nth term for the sequence 7, 4, 1, –2, –5.

Solution:

Problem:

Which term of the A.P. 7, 12, 17, ….. is 87?

Solution:

Problem:

How many terms are there in A.P. 7, 13, 19, …….., 205.

Solution:

Problem:

Check whether –150 is term of the A.P. 11, 8, 5, 2, …….?

Solution:

Problem:

In the following A.P. find the missing terms in the boxes.

(i) 5, , , (ii) –4, , , , , 6

Solution:

Problem:

For what value of n, the nth terms of A.P’s 63, 65, 67, ……… and 3, 10, 17, …… are equal.

Solution:

Problem:

Two A.P.s have the same common difference. If the difference between their 100th terms is 100, what is the difference between their 1000th terms?

Solution:

Problem:

Which term of the arithmetic progression 3, 10, 17, …. will be 84 more than its 13th term?

Solution:

Problem:

Find the 31st term of an A.P. whose 11th term is 38 and the 16th term is 73.

Solution:

Problem:

How many three digit numbers are divisible by 7?

Solution:

Problem:

A sum of Rs 1000 is invested at 8% simple interest per year. Calculate the interest at the end of each year. Do these interests from an AP? If so, find the interest at the end of 30 years.

Solution:

TO FIND nth TERM FROM THE END OF AN A.P.

Problem:

Find the 5th term from the end of the AP, 17, 14, 11, ….., –40

Solution:

Problem:

The sum of the 4th and 8th terms of an A.P. is 24 and sum of 6th & 10th terms is 44. Find the first three term of the AP.

Solution:

Problem:

If the pth term of an A.P. is q and the qth term is p, prove that its nth term is

Solution:

Problem:

If m times the mth term of an A.P. is equal to n times its nth term, show that the (m + n) term of the A.P. is zero.

Solution:

CONDITION FOR TERMS TO BE IN A.P.

Problem:

If are in A.P., find the value of x.

Solution:

Problem:

If the numbers a, b, c, d, e form an A.P., then find the value of .

Solution:

Share this:

Like this:

Find the 18^th term and n^th term for the sequence 7, 4, 1, –2, –5.

(i) 5, , , $\displaystyle 9\frac{1}{2}$ (ii) –4, , , , , 6

Two A.P.s have the same common difference. If the difference between their 100^th terms is 100, what is the difference between their 1000^th terms?

Which term of the arithmetic progression 3, 10, 17, …. will be 84 more than its 13^th term?

Find the 31^st term of an A.P. whose 11^th term is 38 and the 16^th term is 73.

Find the 5^th term from the end of the AP, 17, 14, 11, ….., –40

The sum of the 4^th and 8^th terms of an A.P. is 24 and sum of 6^th & 10^th terms is 44. Find the first three term of the AP.

If the pth term of an A.P. is q and the qth term is p, prove that its nth term is $\displaystyle \left( p+q-n \right).$

If $\displaystyle 2x,x+10,3x+2$ are in A.P., find the value of x.

If the numbers a, b, c, d, e form an A.P., then find the value of $\displaystyle a-4b+6c-4d+e$ .