CBSE 10th Mathematics | Arithmetic Progressions | Sequence and Series

Sequence and Series

Sequence: A sequence is an arrangement of number in a definite order, according to a definite rule.

Terms: Various numbers occurring in a sequence are called terms or element.

Consider the following lists of number:

3, 6, 9, 12, ……………

4, 8, 12, 16, ……………

-3, -2, -1, 0, ……………

In all the list above, we observe that each successive terms are obtained by adding a fixed number to the preceding terms. Such list of numbers is said to form on Arithmetic Progression (AP).

Definition of Arithmetic Progression:

An arithmetic progression is a list of numbers in which each term is obtained by adding a fixed number to the preceding term except the first term.

This fixed number is called the common difference (d) of the Arithmetic Progression

Common difference can be positive, negative or zero.

Let us denote first term of A.P. by a or t, second term by a₂ or t₂ and nth term by a_n or t_n & the common difference by d. Then the Arithmetic Progression becomes

a₁, a₂, a₃ …………………… a_n

where a₂
– a₁ = d

or a₂ = a₁ + d

similarly a₃ = a₂ + d

Note:

In general, an – an-1 = d

an = an-1 + d

Thus

a, a + d, a + 2d, …………………..

forms an A.P. whose first term is ‘a’ & common difference is ‘d’

This is called general form of an A.P.

Finite A.P.: An A.P. containing finite number of terms is called finite A.P.

e.g. 147, 149, 151 ………………….. 163.

Infinite A.P.: An A.P. containing infinite terms is called infinite A.P.

e.g. 6, 9, 12, 15 ………………………..

Problems Based on Sequence and Series

Problem:

What is 18th term of the sequence defined by

$\displaystyle \,{{a}_{n}}=\frac{n(n-3)}{n+4}$

Solution:

We have,

Putting n = 18, we get

$\displaystyle \,{{a}_{18}}=\frac{18\times (18-3)}{18+4}=\frac{18\times 15}{22}=\frac{135}{11}$

Problem:

Let a sequence be defined by

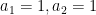$\displaystyle \,{{a}_{1}}=1,{{a}_{2}}=1$ ; $\displaystyle \,{{a}_{n}}={{a}_{n-1}}+{{a}_{n-2}}\,for\,all\,\,n>2$ . Find $\displaystyle \,\frac{{{a}_{n+1}}}{{{a}_{n}}}$ for n = 1, 2, 3, 4,

Solution:

We have,

$\displaystyle \,{{a}_{1}}=1,{{a}_{2}}=1$

and, $\displaystyle \,{{a}_{n}}={{a}_{n-1}}+{{a}_{n-2}}\,for\,all\,\,n>2$

Putting n = 3, 4, and 5, we have

a3 = a2 +a1 = 1 + 1 = 2

a4 = a3 +a2 = 2 + 1 = 3

a5 = a4 +a3 = 3 + 2 = 5

\ we have

a1 = 1, a2 = 1, a3 = 2, a4 = 3 and a5 = 5

Now, putting n = 1, 2, 3 and 4 in $\displaystyle \,\frac{{{a}_{n+1}}}{{{a}_{n}}}$ we have

$\displaystyle \,\frac{{{a}_{2}}}{{{a}_{1}}}=\frac{1}{1}=1$ [\a1 = a2 = 1]

$\displaystyle \,\frac{{{a}_{3}}}{{{a}_{2}}}=\frac{2}{1}=2$ [\a2 = 1 and a3 = 2]

$\displaystyle \,\frac{{{a}_{4}}}{{{a}_{3}}}=\frac{3}{2}$ [\a3 = 2 and a4 = 3]

$\displaystyle \,\frac{{{a}_{5}}}{{{a}_{4}}}=\frac{5}{3}$ [\a4 = 3 and a5 = 5]

Problem:

Which of the following are A.P’s? If they form an A.P., find the common difference d and the next three terms after last given term.

(i) 2, 4, 8, 16, … (ii) $\displaystyle \,\sqrt{2,}\,\,\,\sqrt{8,}\,\,\,\sqrt{18,}$ …

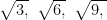(iii) $\displaystyle \,\sqrt{3,}\,\,\,\sqrt{6,}\,\,\,\sqrt{9,\,}$ … (iv) 12, 52, 72, 73, …

Solution:

(i)

2, 4, 8, 16, …

$\displaystyle \begin{array}{l}{{a}_{2}}-{{a}_{1}}=4-2=2\\{{a}_{3}}-{{a}_{2}}=8-4=4\\{{a}_{4}}-{{a}_{3}}=16-8=8\\.............................\\.............................\end{array}$

As the difference between two Consecutive terms is not the same

\ The given sequence is not an A.P.

(ii)

$\displaystyle \begin{array}{l}\sqrt{2,\,}\sqrt{8,\,}\sqrt{18,\,}...\\{{a}_{2}}-{{a}_{1}}=\sqrt{8\,}-\sqrt{2\,}=2\sqrt{2\,}-\sqrt{2\,}=\sqrt{2\,}\\{{a}_{3}}-{{a}_{2}}=\sqrt{18\,}-\sqrt{8\,}=3\sqrt{2\,}-2\sqrt{2\,}=\sqrt{2\,}\\..............................................................\\..............................................................\end{array}$

As the common difference between any two consecutive terms is the same

\ The given sequence is an A.P.

Next three terms are :

$\displaystyle \begin{array}{l}{{a}_{4}}={{a}_{3}}+d=3\sqrt{2\,}+\sqrt{2\grave{\ }\,}=4\sqrt{2\,},\,\,\,\,\,\,\,\,\,\,\,\,\,{{a}_{5}}={{a}_{4}}+d=4\sqrt{2}+\sqrt{2\,}=5\sqrt{2\,}\\{{a}_{6}}={{a}_{5}}+d=5\sqrt{2\,}+\sqrt{2\,}=6\sqrt{2}\end{array}$

(iii)

$\displaystyle \begin{array}{l}\sqrt{3,\,}\sqrt{6,\,}\sqrt{9,\,}...\\{{a}_{2}}-{{a}_{1}}=\sqrt{6\,}-\sqrt{3\,}=\sqrt{3\,}\,(\sqrt{2\,}-1)\\{{a}_{3}}-{{a}_{2}}=\sqrt{9\,}-\sqrt{6\,}=\sqrt{3\,}\,(\sqrt{3\,}-\sqrt{2\,})\\..............................................................\\..............................................................\end{array}$

As the common difference between any two consecutive terms is not the same

\ The given sequence is not an A.P.

(iv)

$\displaystyle \begin{array}{l}{{1}^{2}},{{5}^{2}},{{7}^{2}},73,....\\{{a}_{2}}-{{a}_{1}}={{5}^{2}}-1=25-1=24\\{{a}_{3}}-{{a}_{2}}={{7}^{2}}-{{5}^{2}}=49-25=24\\{{a}_{4}}-{{a}_{3}}=73-49=24\\.................................................\\.................................................\end{array}$

As the common difference between any two consecutive terms is the same

\ The given sequence is an A.P.

Next three terms are :

$\displaystyle {{a}_{7}}=121+24=145$

Problem:

Write the A.P., when the first term a and common difference d is as follows:

(i) a = 10, d = 10 (ii) $\displaystyle a=-1,\,d=\frac{1}{2}$ (iii) $\displaystyle a=-1.25,\,d=0.25$

Solution:

(i) a = 10, d = 10

\ The required A.P. is:

10, 10 + 10, 10 + 2 ´ 10, 10 + 3 ´ 10, …

or 10, 20, 30, 40, …

(ii) $\displaystyle a=-1,\,d=\frac{1}{2}$

\ The required A.P. is:

$\displaystyle -1,\,-1+\frac{1}{2},-1+\frac{1}{2}x2,\,-1+\frac{1}{2}x3,\,...$

or $\displaystyle -\mathbf{1,}\,-\frac{\mathbf{1}}{\mathbf{2}}\mathbf{,}\,\mathbf{0,}\,\frac{\mathbf{1}}{\mathbf{2}}\mathbf{,}\,...$

(iii) $\displaystyle a=-1.25,\,d=-0.25$

\ The required A.P. is:

$\displaystyle -1.25,\,\,-1.25+(-0.25),-1.25+2\times (-0.25),-1.25+3(-0.25),\,...$

or $\displaystyle -1.25,-1.50,-1.75,-2.0,\,...$

Problem:

For the following A.P.’s write the first term and the common difference:

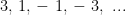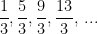(i) $\displaystyle 3,\,1,\,-\,\,1,\,-\,\,3,\,\,...$ (ii) $\displaystyle \frac{1}{3},\frac{5}{3},\frac{9}{3},\frac{13}{3},\,...$ (iii) $\displaystyle 0.6,\,1.7,\,2.8,\,\,...$

Solution:

(i) $\displaystyle 3,\,1,\,-\,\,1,\,-\,\,3,\,\,...$

First term: $\displaystyle {{a}_{1}}=3,\,\,\,d=1-3=-2$

(ii) $\displaystyle \frac{1}{3},\frac{5}{3},\frac{9}{3},\frac{13}{3},\,...$

First term: $\displaystyle {{a}_{1}}=\frac{1}{3},\,\,\,\,\,\,d=\frac{5}{3}-\frac{1}{3}=\frac{4}{3}$

(iii) $\displaystyle 0.6,\,1.7,\,2.8,\,\,...$

First term: $\displaystyle {{a}_{1}}=0.6,\,\,\,d=1.7-0.6=1.1.$

Problem:

Which of the following list of numbers will form an AP?

(i) The amount of air present in the cylinder when a vacuum pump removes each time $\displaystyle \frac{1}{4}$ th of air remaining in the cylinder.

(ii) The cost of digging a well for the first meter is Rs. 150 and rises by Rs. 20 for each succeeding meter.

Solution:

(i)

Let the initial volume = V

Air removed in 1st stage $\displaystyle =\frac{1}{4}V$

Vol. of air left at stage $\displaystyle 1=V-\frac{V}{4}=\frac{3}{4}V$

Air removed in 2nd stage $\displaystyle =\frac{1}{4}\times \frac{3}{4}V=\frac{3}{16}V$

Vol. of air left at stage $\displaystyle 2=\frac{3}{4}V-\frac{3}{16}V=\frac{9}{16}V$

Air removed in 3rd stage = $\displaystyle \frac{1}{4}\times \frac{9}{16}V=\frac{9}{64}V$

Vol. of air left at stage $\displaystyle 3=\frac{9}{16}V-\frac{9}{64}V=\frac{27}{64}V$

Now, the difference between the volumes of air left in the initial stage and stage 1 is given by

$\displaystyle V-\frac{3V}{4}=\frac{1}{4}V$

Similarly, the difference between the volumes of air left in the stage 1 and stage 2 is given by

$\displaystyle \frac{3}{4}V-\frac{9}{16}V=\frac{3}{16}V$

Also, such difference between the stage 2 and stage 3 is given by $\displaystyle \frac{9}{16}V-\frac{27}{64}V=\frac{9}{64}V$

Since the difference in the volumes at the first three stages are $\displaystyle \frac{1}{4}V,\,\frac{3}{16}V\,\,and\,\,\,\frac{9}{64}V$

which are not equal, it is not an A.P.

(ii) Since the cost of digging a well rises by Rs. 20

\ the cost of digging well becomes:

150 + (150 + 20) + (150 + 40) + ………..

i.e., 150 + 170 + 190 + ……………

\ The above series forms an A.P.

CBSE Tutorials

CBSE 10th Mathematics | Arithmetic Progressions | Sequence and Series

Sequence and Series

Definition of Arithmetic Progression:

Problems Based on Sequence and Series

Problem:

What is 18th term of the sequence defined by

$\displaystyle \,{{a}_{n}}=\frac{n(n-3)}{n+4}$

Solution:

Problem:

Let a sequence be defined by

$\displaystyle \,{{a}_{1}}=1,{{a}_{2}}=1$ ; $\displaystyle \,{{a}_{n}}={{a}_{n-1}}+{{a}_{n-2}}\,for\,all\,\,n>2$ . Find $\displaystyle \,\frac{{{a}_{n+1}}}{{{a}_{n}}}$ for n = 1, 2, 3, 4,

Solution:

Problem:

Which of the following are A.P’s? If they form an A.P., find the common difference d and the next three terms after last given term.

(i) 2, 4, 8, 16, … (ii) $\displaystyle \,\sqrt{2,}\,\,\,\sqrt{8,}\,\,\,\sqrt{18,}$ …

(iii) $\displaystyle \,\sqrt{3,}\,\,\,\sqrt{6,}\,\,\,\sqrt{9,\,}$ … (iv) 12, 52, 72, 73, …

Solution:

Problem:

Write the A.P., when the first term a and common difference d is as follows:

(i) a = 10, d = 10 (ii) $\displaystyle a=-1,\,d=\frac{1}{2}$ (iii) $\displaystyle a=-1.25,\,d=0.25$

Solution:

Problem:

For the following A.P.’s write the first term and the common difference:

(i) $\displaystyle 3,\,1,\,-\,\,1,\,-\,\,3,\,\,...$ (ii) $\displaystyle \frac{1}{3},\frac{5}{3},\frac{9}{3},\frac{13}{3},\,...$ (iii) $\displaystyle 0.6,\,1.7,\,2.8,\,\,...$

Solution:

Problem:

Which of the following list of numbers will form an AP?

(i) The amount of air present in the cylinder when a vacuum pump removes each time $\displaystyle \frac{1}{4}$ th of air remaining in the cylinder.

(ii) The cost of digging a well for the first meter is Rs. 150 and rises by Rs. 20 for each succeeding meter.

Solution:

Like this:

CBSE 10th Mathematics | Arithmetic Progressions | Sequence and Series

Sequence and Series

Definition of Arithmetic Progression:

Problems Based on Sequence and Series

Problem:

What is 18th term of the sequence defined by

Solution:

Problem:

Let a sequence be defined by

; . Find for n = 1, 2, 3, 4,

Solution:

Problem:

Which of the following are A.P’s? If they form an A.P., find the common difference d and the next three terms after last given term.

(i) 2, 4, 8, 16, … (ii) …

(iii) … (iv) 12, 52, 72, 73, …

Solution:

Problem:

Write the A.P., when the first term a and common difference d is as follows:

(i) a = 10, d = 10 (ii) (iii)

Solution:

Problem:

For the following A.P.’s write the first term and the common difference:

(i) (ii) (iii)

Solution:

Problem:

Which of the following list of numbers will form an AP?

(i) The amount of air present in the cylinder when a vacuum pump removes each time th of air remaining in the cylinder.

(ii) The cost of digging a well for the first meter is Rs. 150 and rises by Rs. 20 for each succeeding meter.

Solution:

Share this:

Like this:

$\displaystyle \,{{a}_{1}}=1,{{a}_{2}}=1$ ; $\displaystyle \,{{a}_{n}}={{a}_{n-1}}+{{a}_{n-2}}\,for\,all\,\,n>2$ . Find $\displaystyle \,\frac{{{a}_{n+1}}}{{{a}_{n}}}$ for n = 1, 2, 3, 4,

(i) 2, 4, 8, 16, … (ii) $\displaystyle \,\sqrt{2,}\,\,\,\sqrt{8,}\,\,\,\sqrt{18,}$ …

(iii) $\displaystyle \,\sqrt{3,}\,\,\,\sqrt{6,}\,\,\,\sqrt{9,\,}$ … (iv) 12, 52, 72, 73, …

(i) a = 10, d = 10 (ii) $\displaystyle a=-1,\,d=\frac{1}{2}$ (iii) $\displaystyle a=-1.25,\,d=0.25$

(i) $\displaystyle 3,\,1,\,-\,\,1,\,-\,\,3,\,\,...$ (ii) $\displaystyle \frac{1}{3},\frac{5}{3},\frac{9}{3},\frac{13}{3},\,...$ (iii) $\displaystyle 0.6,\,1.7,\,2.8,\,\,...$

(i) The amount of air present in the cylinder when a vacuum pump removes each time $\displaystyle \frac{1}{4}$ th of air remaining in the cylinder.