Sum of n terms of an Arithmetic Progression
Let a be the first term and d be the common difference of an A.P. is the last term where l = a + (n
– 1) d.
Sum of first n terms of the given A.P. is given by
…(i)
Writing in reverse order
…(ii)
Adding (i) and (ii) we get
[
l = a + (n – 1)d]
where an = a + (n – 1)d
Solved Problems based on Sum of n terms of an Arithmetic Progression
Problem:
Find the sum of the first
(i) 100 natural numbers
(ii)n natural numbers.
Solution:
(i)
Here,
Using the formula
\
(ii)
Here,
=
=
Problem:
The sum of the first 17 terms of an arithmetic sequence is 187. If 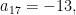 find a and d
find a and d
Solution:
Using with n = 17
\
Þ
Þ …(i)
Now,
Þ
Þ [from (i)]
Þ
Þ
d = – 3
Problem:
(i)Given  find a and S12.
find a and S12.
(ii)Given 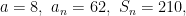 find n and d.
find n and d.
(iii)Given 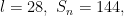 n = 9, find a.
n = 9, find a.
Solution:
(i)
Given find a and S12.

\
or or a = 4
\
(ii)
Given find n and d.
Þ
Also 
Þor
\
(iii)
Given n = 9, find a.
\

or 32 = a + 28
Þa = 32 – 28 = 4
Problem:
The first term of an A.P. is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
Solution:
Here,
\
Þ
Also = 45
\an =
Þ
Þ
Hence, number of terms(n)
Problem:
If the sum of 7 term of an A.P. is 49 and that of 17 term is 289, find the sum of n terms.
Solution:
[Given]
Þ
or…(i)
Also
or…(ii)
Subtracting (i) from (ii), we get
or d = 2
Putting d = 2 in (i), we get a = 7 – 3 ´ 2 = 1
\
Problem:
Find the sum of positive integers less than 400.
Solution:
Positive integers less than 400 are
1, 2, 3, 4, 5, …., 399
Here,
\
Þ
or
\
Problem:
Find the sum of the odd numbers between 0 and 50.
Solution:
Odd numbers between 0 and 50 are
1, 3, 5, 7, …, 49
Here,
\
Þ or n = 25
\
Problem:
A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs 200 for the first day, Rs 250 for the second day, Rs 300 for the third day, etc. the penalty for each succeeding day being Rs. 50 more than for the preceding day. How much does a delay of 30 days cost the contractor?
Solution:
Here, Rs 200, d = Rs. 50, n = 30
\
= Rs 27750
\Delay of 30 days will cost Rs. 27750 as penalty to the contractor.
Problem:
Raghav buys a shop for Rs 120000. He pays half of the amount in cash and agrees to pay the balance in 12 annual installments of Rs. 5000 each. If the rate of interest is 12% and he pays with the instalment the interest due on the unpaid amount, find the total cost of the shop.
Solution:
Total cost of the shop = Rs. 120000
Cash = Rs. 60000
Interest for 1st installment = Rs Rs. 7200
Interest for 2nd installment = Rs Rs. 6600
……………………………………………………..
……………………………………………………..
So, the interest for 12 installments will be
7200, 6600, 6000, 5400, 4800, …., 600
Writing in the reverse order we have
600, 1200, 1800, …., 7200
Here, a = Rs. 600, d = Rs. (1200 – 600) = Rs. 600, = Rs. 7200
\Sum of interest paid Rs. 46800
So, total cost of the shop = Rs. (60000 + 60000) + Rs. (46800)
= 166800
Problem:
200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on (See figure). In how many rows the 200 logs are placed and how many logs are in the top row.

Solution:
Here,
either or
(i) Taking
The number of logs in 25th row is
Which is not possible as number of logs can not be negative
\ is rejected
(ii) Taking
The number of logs in 16th row is
\ 5 logs are placed in 16th row
Problem:
Find the sum of the first 25 terms of an A.P. whose nth term is given by 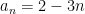 .
.
Solution:
Here, 
Þ
Þd. = –3
\
Hence
Problem:
Find the common difference of an A.P. whose first term is 1 and the sum of the first four term is one-third the sum of the next four terms.
Solution:
Let d be the common difference of the A.P. Given that a = 1 and
According to Problem:
…(i)
Adding to both sides of (i), we get
Þ
or
Now,
and
According to the Problem:
Þ16 + 24d = 8 + 28d
or
Problem:
How many terms of the sequence 18, 16, 14, …. should be taken so that their sum is zero?
Solution:
Here
Þ
Þ
Þ
Þor
Þn = 19
Hence, 19 terms of the sequence 8, 16, 14…. should be taken so that their sum is zero.
Problem:
A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete.
Each step has a rise of  m and a tread of
m and a tread of  m see figure Calculate the total volume of concrete required to built the terrace.
m see figure Calculate the total volume of concrete required to built the terrace.

Solution:
Volume of concrete needed to make first step
=m3
= m3
Volume of concrete needed to make second step
m3
= m3
Volume of concrete needed to make third step
m3
m3
Here
\Total volume of concrete needed to make such 15 steps
=
m3.
Problem:
A spiral is made up of successive semicircles, with centres alternatively at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles? Take 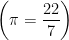

Solution:
= 0.5 cm
= 1.0 cm
= 1.5 cm
Length of Ist spiral = pr1 (circumference of semicircle)
=
Length of IInd spiral = pr2
=
Length of IIIrd spiral = pr3
=
\
Length of spiral up of 13 consecutive semicircles
= 143 cm
Problem:
The sum of the third and the seventh terms of an A.P. is 6 and their product is 8. Find the sum of first sixteen terms of the A.P.
Solution:
Let a be the first term and d the common difference
According to question
…(i)
[Given]
[from (i)]
Þ
Þ
Þ
Þ or
Taking
Þ
\
Taking Þ
\
Selection of Terms in A.P.
Sometimes certain number of terms in A.P. are required. The following ways of selecting terms are convenient.
Number of terms common difference
3d
42d
5d
62d
Problem:
A sum of Rs 280 is to be used to award four prizes. If each prize after the first is Rs. 20 less than the next most valuable one, find the value of each of the prize.
Solution:
Each prize is Rs. 20 less than the next most valuable one
Þ
d = Rs. 20
\ The four prizes are:
Þ[
d = 20]
Þ
According to question, we have
Þa = 70
Hence the four prizes are:
70 – 60 = Rs.10; 70 – 20 = Rs. 50; 70 + 20 = Rs. 90; 70 + 60 = Rs. 130.
Problem:
The sum of three numbers in A.P. is -3, and their product is 8. Find the numbers.
Solution:
Let the number be . Then
Sum

 …(i)
…(i)
Now, Product = 8
Þ
Þ
Þ [from (i)]
Þ
If d = 3 the numbers are If d = -3, the numbers are 2, -1, -4.
Thus, the numbers are or
Problem:
Divide 32 into four parts which are in A.P. such that the product of extremes is to the product of means is 7:15.
Solution:
Let the four parts be and
. Then, sum = 32
Þ
According to question
Þ
Þ
Þ
Thus, the four parts are and
i.e., 2, 6, 10, 14.
Problem:
The sums of n terms of three arithmetical progressions are 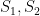 and
and  . The first term of each is unity and the common differences are 1, 2, and 3 respectively. Prove that
. The first term of each is unity and the common differences are 1, 2, and 3 respectively. Prove that 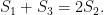
Solution:
According to Problem:
= sum of n term of an A.P. with a = 1 and d = 1
Þ
sum of n terms of an A.P. with a = 1 and d = 2
Þ
sum of n terms of an A.P. with a = 1 and d = 3
Þ
Now,
and
Hence,