CBSE 10th Mathematics | Coordinate Geometry | Area of A Triangle

Coordinate Geometry | Area of A Triangle

The area of a DABC with vertices $\displaystyle A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $\displaystyle C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by area $\displaystyle \left( \Delta ABC \right)=\left| \frac{1}{2}\left\{ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right\} \right|.$

Proof :

Let $\displaystyle A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $\displaystyle C\left( {{x}_{3}},{{y}_{3}} \right)$ be the vertices of the given DABC.

Draw AP, BM and CN perpendiculars to the x-axis.

Then, $\displaystyle MP=\left( {{x}_{1}}-{{x}_{2}} \right),PN\left( {{x}_{3}}-{{x}_{1}} \right)$

and MN = $\displaystyle \left( {{x}_{3}}-{{x}_{2}} \right)$

\ area of DABC

= ar (trap. BMPA) + ar (trap.. APNC) – ar (trap. BMNC)

= $\displaystyle \left\{ \frac{1}{2}\left( AP+BM \right)\times MP \right\}+\left\{ \frac{1}{2}\left( AP+CN \right)\times PN \right\}-\left\{ \frac{1}{2}\left( BM+CN \right)\times MN \right\}$

= $\displaystyle \frac{1}{2}\left( {{y}_{1}}+{{y}_{2}} \right)\left( {{x}_{1}}-{{x}_{2}} \right)+\frac{1}{2}\left( {{y}_{1}}+{{y}_{3}} \right)\left( {{x}_{3}}-{{x}_{1}} \right)-\frac{1}{2}\left( {{y}_{2}}+{{y}_{3}} \right)\left( {{x}_{3}}-{{x}_{2}} \right)$

= $\displaystyle \frac{1}{2}\left[ {{x}_{1}}\left( {{y}_{1}}+{{y}_{2}}-{{y}_{1}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{2}}+{{y}_{3}}-{{y}_{1}}-{{y}_{2}} \right)+{{x}_{3}}\left( {{y}_{1}}+{{y}_{3}}-{{y}_{2}}-{{y}_{3}} \right) \right]$

$\displaystyle =\frac{1}{2}\left\{ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right\}.$

Since the area is never negative, we have

area $\displaystyle \left( \Delta ABC \right)=\frac{1}{2}\left| \left\{ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right\} \right|$

Condition for Collinearity of Three Points

Let the given points be $\displaystyle A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and $\displaystyle \left( {{x}_{3}},{{y}_{3}} \right)$ .

Then, A, B and C are collinear

Þ area of DABC = 0

Þ $\displaystyle \frac{1}{2}.\left\{ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right\}=0$

Þ $\displaystyle {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right)=0$

Question:

Find the area of a triangle whose vertices are (1, –1), (–4, 6) and (–3, –5).

Solution:

The area of the triangle formed by the vertices A(1, –1), B(–4, 6) and C(–3, –5) is given by

$\displaystyle \frac{1}{2}[1(6+5)+(-4)(-5+1)+(-3)(-1-6)]$ = $\displaystyle \frac{1}{2}(11+16+21)=24$

So, the area of the triangle is 24 square units.

Question:

Find the value of k if the points A(2, 3), B(4, k) and C(6, –3) are collinear.

Solution:

Since the given points are collinear, the area of the triangle will be 0,

Þ $\displaystyle \frac{1}{2}[2(k+3)+4(-3-3)+6(3-k)]=0$

Þ $\displaystyle \frac{1}{2}[2k+6-24+18-6k]=0$

Þ $\displaystyle \frac{1}{2}(-4k)=0$

Therefore, k = 0

Question:

If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.

Solution:

By joining B to D, two triangles ABD and BCD are formed.

Now the area of DABD

= $\displaystyle \frac{1}{2}(50+8+48)=\frac{106}{2}=53$ square units

Also, the area of DBCD

= $\displaystyle \frac{1}{2}[-4(-6-5)-1(5+5)+4(-5+6)]$

= $\displaystyle \frac{1}{2}(44-10+4)=19$ square units

So, the area of quadrilateral ABCD = 53 + 19 = 72 square units.

Question:

Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear.

Solution:

Let D be the area of the triangle formed by the points (a, b + c), (b, c + a) and (c, a + b)

Þ $\displaystyle \Delta =\frac{1}{2}\left| \left\{ a(c+a)+b(a+b)+c(b+c) \right\}-\left\{ b(b+c)+c(c+a)+a(a+b) \right\} \right|$

Þ $\displaystyle \Delta =\frac{1}{2}\left| (ac+{{a}^{2}}+ab+{{b}^{2}}+bc+{{c}^{2}})-({{b}^{2}}+bc+{{c}^{2}}+ca+{{a}^{2}}+ab) \right|$

Þ D = 0

Since area is zero \ the given points are collinear.

Question:

Find the
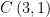value of k for which the area formed by the triangle with vertices $\displaystyle A\left( k,2k \right),B\left( -2,6 \right)$ and $\displaystyle C\left( 3,1 \right)$ is 5 square units.

Solution:

The vertices of the given DABC are $\displaystyle A\left( k,2k \right),B\left( -2,6 \right)$ and $\displaystyle C\left( 3,1 \right)$ .

\
$\displaystyle {{x}_{1}}=k,\,{{y}_{1}}=2k,{{x}_{2}}=-2,{{y}_{2}}=6$ and $\displaystyle {{x}_{3}}=3,{{y}_{3}}=1$

Area of $\displaystyle \Delta ABC=\frac{1}{2}\left| \left\{ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right\} \right|$

= $\displaystyle \frac{1}{2}\left| k\left( 6-1 \right)-2\left( 1-2k \right)+3\left( 2k-6 \right) \right|$

= $\displaystyle \frac{1}{2}\left| 5k-2+4k+6k-18 \right|$

= $\displaystyle \frac{1}{2}\left| 15k-20 \right|$ sq units.

But, area of DABC = 5 sq units [given]

\ $\displaystyle \frac{1}{2}\left| 15k-20 \right|=5\,\,\,\,\,\,\Rightarrow \,\,\,\,\,\left| 15k-20 \right|=10$

Þ
$\displaystyle \left( 15k-20 \right)=10$ or $\displaystyle \left( 15k-20 \right)=-10$

Þ
$\displaystyle k=2$ or $\displaystyle k=\frac{2}{3}$ .

Hence, $\displaystyle k=2$ or $\displaystyle k=\frac{2}{3}$

CBSE Tutorials

CBSE 10th Mathematics | Coordinate Geometry | Area of A Triangle

Coordinate Geometry | Area of A Triangle

Question:

Find the area of a triangle whose vertices are (1, –1), (–4, 6) and (–3, –5).

Solution:

Question:

Find the value of k if the points A(2, 3), B(4, k) and C(6, –3) are collinear.

Solution:

Question:

If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.

Solution:

Question:

Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear.

Solution:

Question:

Find the
value of k for which the area formed by the triangle with vertices $\displaystyle A\left( k,2k \right),B\left( -2,6 \right)$ and $\displaystyle C\left( 3,1 \right)$ is 5 square units.

Solution:

Like this:

CBSE 10th Mathematics | Coordinate Geometry | Area of A Triangle

Coordinate Geometry | Area of A Triangle

Question:

Find the area of a triangle whose vertices are (1, –1), (–4, 6) and (–3, –5).

Solution:

Question:

Find the value of k if the points A(2, 3), B(4, k) and C(6, –3) are collinear.

Solution:

Question:

If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.

Solution:

Question:

Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear.

Solution:

Question:

Find the value of k for which the area formed by the triangle with vertices and is 5 square units.

Solution:

Share this:

Like this:

Find the
value of k for which the area formed by the triangle with vertices $\displaystyle A\left( k,2k \right),B\left( -2,6 \right)$ and $\displaystyle C\left( 3,1 \right)$ is 5 square units.