CBSE Tutorials

CBSE 10th Mathematics | Similar Triangles | Criteria For Similarity Of Two Triangles

Similar Triangles | Criteria for Similarity of Two Triangles

Two triangles are said to be similar if

(i) their corresponding angles are equal and

(ii) their corresponding sides are in the same ratio (or proportional).

Thus, two triangles ABC and \displaystyle A\prime B\prime C\prime are similar if

(i)    \displaystyle \angle A=\angle A\prime , \displaystyle \angle B=\angle B\prime , \displaystyle \angle C=\angle C\prime and

(ii)    \displaystyle \frac{AB}{A\prime B\prime }=\frac{BC}{B\prime C\prime }=\frac{CA}{C\prime A\prime }

In this section, we shall make use of the theorems discussed in earlier sections to derive some criteria for similar triangles which in turn will imply that either of the above two conditions can be used to define the similarity of two triangles.

CHARACTERISTIC PROPERTY 1 (AAA SIMILARITY)

Theorem: If in two triangles, the corresponding angles are equal, then the triangles are similar.

Given:

Two triangles ABC and DEF in which \displaystyle \angle A=\angle D, \displaystyle \angle B=\angle E, \displaystyle \angle C=\angle F.

To prove:

DABC ~ DDEF

Proof:

Case 1: When AB = DE

In triangles ABC and DEF, we have

\displaystyle \angle A=\angle D            [Given]

AB = DE             [Given]

\displaystyle \angle B=\angle E            [Given]

\    \displaystyle \Delta ABC\cong \Delta DEF        [By ASA congruency]

Þ    BC = EF and AC = DF    [c.p.c.t.]

Thus,    \displaystyle \frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}        [corresponding sides of similar Ds are proportional]

Hence, \displaystyle \Delta ABC\tilde{\ }\Delta DEF

Case 2: When AB < DE

Let P and Q be points on DE and DF respectively such that DP = AB and DQ = AC. Join PQ.

In DABC and DDPQ, we have

AB = DP             [By construction]

ÐA = ÐD            [Given]

AC =DQ             [By construction]

\    DABC \displaystyle \cong \displaystyle \Delta DPQ        [By SAS congruency]

\    ÐABC = ÐDPQ        [c.p.c.t.]        …(i)

But    ÐABC = ÐDEF        [Given]            …(ii)

\     ÐDPQ = ÐDEF         [c.p.c.t.]

But    ÐDPQ and ÐDEF are corresponding angles.

Þ    PQ || EF

\    \displaystyle \frac{DP}{DE}=\frac{DQ}{DF}            [Corollary to BPT Theorem]

\    \displaystyle \frac{AB}{DE}=\frac{AC}{DF}            [\displaystyle \because DP = AB and DQ = AC (by construction)]

Similarly \displaystyle \frac{AB}{DE}=\frac{BC}{EF}

\    \displaystyle \frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}

Hence, DABC ~ DDEF.

Case 3:    When AB > DE

Let P and Q be points on AB and AC respectively such that AP = DE and AQ = DF. Join PQ.

In DAPQ and DDEF, we have

AP = DE    [By construction]

AQ = DF     [By construction]

ÐA = ÐD    [Given]

\    DAPQ \displaystyle \cong DDEF     [By SAS congruency]

\    ÐAPQ = ÐDEF     [c.p.c.t.]        …(i)

But    ÐDEF = ÐABC    [Given]            …(ii)

From (i) and (ii) we have

\    ÐAPQ = ÐABC

But     ÐAPQ and ÐABC are corresponding angles

\    PQ || BC

\    \displaystyle \frac{AP}{AB}=\frac{AQ}{AC}        [Corollary to BPT Theorem]

\    \displaystyle \frac{DE}{AB}=\frac{DF}{AC}        [\displaystyle \because AP = DE and AQ = DF (by construction)]

Similarly,     \displaystyle \frac{DE}{AB}=\frac{EF}{BC}

Thus,         \displaystyle \frac{DE}{AB}=\frac{EF}{BC}=\frac{DF}{AC}

or        \displaystyle \frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}

Hence,     DABC ~ DDEF.

CHARACTERISTIC PROPERTY 2 (SSS SIMILARITY)

Theorem: If the corresponding sides of two triangles are proportional, then they are similar.

Given:

Two triangles ABC and DEF such that \displaystyle \frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}

To prove:    DABC ~ DDEF

Construction: Let P and Q be points on DE and DF respectively such that DP = AB and      DQ = AC. Join PQ

Proof:         \displaystyle \frac{AB}{DE}=\frac{AC}{DF}            [Given]

Þ     \displaystyle \frac{DP}{DE}=\frac{DQ}{DF}                        …(i)

[\displaystyle \because DP = AB and DQ = AC (by construction)]

In DDEF, we have

\displaystyle \frac{DP}{DE}=\frac{DQ}{DF}            [From (i)]

\    PQ || EF             [By the converse of BPT]

\    ÐDPQ = ÐDEF and ÐDQP = ÐDFE [Corresponding angles]

\    DDPQ = ~ DDEF         [By AA similarity]    …(ii)

\    \displaystyle \frac{DP}{DE}=\frac{PQ}{EF}

or    \displaystyle \frac{AB}{DE}=\frac{PQ}{EF}            [\displaystyle \because DP = AB]        …(iii)

But    \displaystyle \frac{AB}{DE}=\frac{BC}{EF}             [given]            …(iv)

From equations (iii) and (iv), we have \displaystyle \frac{PQ}{EF}=\frac{BC}{EF}

Þ    BC = PQ                         …(v)

In DABC and DDPQ, we have

AB = DP [By construction]

AC = DQ [By construction]

BC = PQ         [By (v)]

\    DABC \displaystyle \cong DDPQ     [by SSS congruency]

Þ    DABC ~ DDPQ     [\displaystyle \because DABC \displaystyle \cong DPQ Û
DABC ~ DDPQ] … (vi)

From equation (ii) and (vi), we get

DABC ~ DDEF

CHARACTERISTIC PROPERTY 3 (SAS SIMILARITY)

Theorem 5: If one angle of a triangle is equal to one angle of the other and the sides including these angles are proportional than the two triangles are similar.

Given:     Two triangle ABC and DEF such that ÐA = ÐD and \displaystyle \frac{AB}{DE}=\frac{AC}{DF}

To prove:
DABC ~ DDEF

Construction: Let P and Q be points on DE and DF respectively such that DP = AB and      DQ = AC. Join PQ.

Proof:    In DABC and DDPQ, we have

AB = DP    [By construction]

AC = DQ    [By construction]

ÐA = ÐD    [Given]

\    DABC @
DDPQ    [By SAS congruency]        …(i)

Now,     \displaystyle \frac{AB}{DE}=\frac{AC}{DF}                        …(ii)

\    \displaystyle \frac{DP}{DE}=\frac{DQ}{DF}        [\displaystyle \because AB = DP and AC = DQ (by construction)]

In DDEF, we have

\displaystyle \frac{DP}{DE}=\frac{DQ}{DF}        [From (ii)]

\    PQ || EF        [By the converse of BPT]

\    ÐDPQ = ÐDEF and ÐDQP = ÐDFE    [Corresponding angles]

\    DDPQ ~ DDEF        [By AA similarity]         …(iii)

From equations (i) and (iii), we get

DABC ~
DDEF.

Question:

Examine each pair of triangles in figure and state which pair of triangles are similar. Also, state the similarity criterion used and write the similarity relation in symbolic form.

Solution:

(i)

In triangles ABC and PQR, we observe that

ÐA = ÐQ = 40°, ÐB = ÐP = 60° and ÐC = ÐR = 80°

Therefore, by AAA-criterion of similarity

DBAC ~ DPQR

(ii)

In triangle PQR and DEF, we observe that

\displaystyle \frac{PQ}{DE}=\frac{QR}{EF}=\frac{PR}{DF}=\frac{1}{2}

Therefore, by SSS-criterion of similarity, we have

DPQR ~ DDEF

(iii)

In D‘s MNP and EFG, we observe that

\displaystyle \frac{NP}{FG}=\frac{MP}{EG}\ne \frac{MN}{EF}

Therefore, these two triangles are not similar as they do not fulfill SSS-criterion of similarity.

(iv)

In D‘s DEF and MNP, we have

ÐD = ÐM = 70°

ÐE = ÐN = 80°    [\displaystyle \because ÐN = 180° – ÐM – ÐP = 180° – 70° – 30° = 80°]

So, by AA-criterion of similarity DDEF ~ DMNP.

Question:

Prove that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.

Solution:


Given:

DABC and DPQR in which BC = a, CA = b, AB = c and QR = p, RP = q, PQ = r.

Also, DABC ~ D PQR.

To Prove:    \displaystyle \frac{a}{p}=\frac{b}{q}=\frac{c}{r}=\frac{a+b+c}{p+q+r}

Proof:

Since DABC and DPQR are similar, therefore their corresponding sides are proportional.

Let     \displaystyle \frac{a}{p}=\frac{b}{q}=\frac{c}{r}=k                        …(i)

Þ    a = kp, b = kq and c = kr

\    \displaystyle \frac{\text{perimeter of }\Delta \text{ABC}}{\text{perimeter}\ \text{of }\Delta \text{PQR}}=\frac{a+b+c}{p+q+r}=\frac{kp+kq+kr}{p+q+r}=\frac{k(p+q+r)}{(p+q+r)}

= \displaystyle \frac{k(p+q+r)}{(p+q+r)}=k                    … (ii)

From (i) and (ii), we get \displaystyle \frac{a}{p}=\frac{b}{q}=\frac{c}{r}=\frac{a+b+c}{p+q+r}=\frac{\text{perimeter of}\ \Delta \text{ABC }}{\text{perimeter of }\Delta \text{PQR}}

[each equal to k]

Question:

A vertical stick 12m long casts a shadow 8m long on the ground. At the same time a tower casts the shadow 40m long on the ground. Determine the height of the tower.

Solution:

Let AB be the vertical stick and AC be its shadow. Also, let DE be the vertical tower and DF be its shadow. Join BC and EF.

Let DE = x metres.

We have,

AB = 12m, AC = 8m, and DF = 40m.

In DABC and DDEF, we have

ÐA = ÐD = 90° and ÐC = ÐF        [Angle of elevation of the sun]

Therefore, by AA-criterion of similarity

DABC ~ DDEF

Þ    \displaystyle \frac{AB}{DE}=\frac{AC}{DF}

Þ    \displaystyle \frac{12}{x}=\frac{8}{40}\Rightarrow \frac{12}{x}=\frac{1}{5}\Rightarrow x=60 metres

Question:

In the given figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ^
BC and EF ^ AC, prove that DABD ~ ECF.

Solution:

Given:

An isosceles DABC in which AB = AC, E is a point on CB produced, AD ^ BC and EF ^ AC.

To prove:

DABD ~ DECF

Proof:

In DABC, since AB = AC,

therefore ÐC = ÐB             [Ðs opposite to equal sides are equal]

In DABD and DECF


ÐB = ÐC            [Proved above]

and    ÐEFC = ÐADB        [each 90°]

\    DABD ~ ECF            [AA similarity]

Question:

E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F. Prove that DABE ~ DCFB.


Solution:

Given:

E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F

To prove:
DABE ~ DCFB

Proof: In D‘s ABE and CFB, we have

ÐAEB = ÐCBF            [Alternate angles]

ÐA = ÐC                [Opposite angles of a parallelogram]

\    DABE ~ DCFB.        [By AA similarity]

Question:

In figure, if 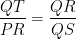\displaystyle \frac{QT}{PR}=\frac{QR}{QS} and Ð1 = Ð2. Prove that DPQS ~ DTQR.

Solution:

Given: \displaystyle \frac{QT}{PR}=\frac{QR}{QS} and Ð1 = Ð2

To prove:
DPQS ~ DTQR

Proof: We have,

\displaystyle \frac{QT}{PR}=\frac{QR}{QS}    [Given]

Þ    \displaystyle \frac{QT}{QR}=\frac{PR}{QS}                            …(i)

We also have,

Ð1 = Ð2                            [Given]

Þ    PR = PQ [Sides opposite to equal angles are equal]        …(ii)

From (i) and (ii), we get

\displaystyle \frac{QT}{QR}=\frac{PQ}{QS}

Þ    \displaystyle \frac{PQ}{QT}=\frac{QS}{QR}

Thus, in triangles PQS and TQR, we have

\displaystyle \frac{PQ}{QT}=\frac{QS}{QR} and \displaystyle \angle PQS=\angle TQR=\angle Q

\    DPQS ~ DTQR.    [By SAS similarity]

Question:

In figure, if DABE @ DACD, prove that DADE ~ DABC.


Solution:

Given: DABE @ DACD

To prove:
DADE ~ DABC

Proof: Since DABE @ DACD

\    AB = AC [cpct]…. (i)

and,    AD = AE                    …. (ii)

Also,     \displaystyle \frac{AB}{AD}=\frac{AC}{AE}    [From (i) and (ii)]

Þ    \displaystyle \frac{AB}{AC}=\frac{AD}{AE}                    … (iii)

Thus, in triangles ADE and ABC, we have

\displaystyle \frac{AB}{AC}=\frac{AD}{AE}

and,    ÐBAC = ÐDAE                [Common]

Hence, by SAS criterion of similarity.

DADE ~ DABC

Question:

In figure, AD and CE are two altitudes of DABC. Prove that

(i)    DAEF ~ DCDF

(ii)    DABD ~ DCBE

(iii)    DAEF ~ DADB

(iv)    DFDC ~ DBEC

Solution:

Given: AD and CE are two altitudes of DABC

To prove:

(i)    DAEF ~ DCDF

(ii)    DABD ~ DCBE

(iii)    DAEF ~ DADB

(iv)    DFDC ~ DBEC

Proof:    

(i)

In triangles AEF and CDF, we have

ÐAEF = ÐCDF = 90°            [\displaystyle \because CE ^ AB and AD ^ BC]

ÐAFE = ÐCFD            [Vertically opposite angles]

\    DAEF ~ DCDF             [By AA similarity]

(ii)

In D‘s ABD and CBE, we have

ÐABD = ÐCBE = ÐB            [Common angle]

ÐADB = ÐCEB = 90°            [\displaystyle \because AD ^ BC and CE ^ AB]

\    DABD ~ DCBE                [By AA similarity]

(iii)

In D‘s AEF and ADB, we have

ÐAEF = ÐADB = 90°            [\displaystyle \because AD ^ BC and CE ^ AB]

ÐFAE = ÐDAB            [Common angle]

\    DAEF ~ DADB                [By AA similarity]

(iv)

In D‘s FDC and BEC, we have

ÐFDC = ÐBEC = 90°            [\displaystyle \because AD ^ BC and CE ^ AB]

ÐFCD = ÐECB            [Common angle]

\    DFDC ~ DBEC                [By AA similarity]

Question:

In figure, if BD ^ AC and CE ^ AB, prove that

(i)    DAEC ~ DADB

(ii) 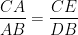   \displaystyle \frac{CA}{AB}=\frac{CE}{DB}

Solution:

Given: BD ^ AC and CE ^ AB

To prove:

(i)    DAEC ~ DADB

(ii)    \displaystyle \frac{CA}{AB}=\frac{CE}{DB}

Proof:

(i)

In D‘s AEC and ADB,

we have

ÐAEC = ÐADB = 90°                [\displaystyle \because CE ^ AB and BD ^ AC]

and,    ÐEAC = ÐDAB                [Each equal to ÐA]

\    D AEC ~ DADB                [By AA similarity]

(ii)

We have,

DAEC ~ DADB                [Proved above]

Þ    \displaystyle \frac{CA}{BA}=\frac{EC}{DB}

Þ    \displaystyle \frac{CA}{AB}=\frac{CE}{DB}

Question:

If CD and GH (D and H lie on AB and FE) are respectively bisectors of ÐACB and ÐEGF and DABC ~ DFEG, prove that

(i) 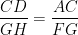   \displaystyle \frac{CD}{GH}=\frac{AC}{FG}

(ii)    DDCB ~ DHGE

Solution:

Given:

(i)    DABC ~ DFEG

(ii)    CD, the bisector of ÐACB meets AB at D and

(iii)    GH, the bisector of ÐEGF meets FE at H.

To prove:

(i)    \displaystyle \frac{CD}{GH}=\frac{AC}{FG}

(ii)    DDCB ~ DHGE

Proof:

(i)

DABC ~ DFEG            [Given]

\    ÐBAC = ÐEFG            …(i)

ÐABC = ÐFEG            …(ii)

and    ÐACB = ÐFGE            …(iii)

[Corresponding angles of similar triangles]

\    \displaystyle \frac{1}{2}\angle ACB=\frac{1}{2}\angle FGE

\    ÐACD = ÐFGH            …(iv)

[As CD is the bisector of ÐACB]

and    ÐDCB = ÐHGE            …(v)

[As GH is the bisector of ÐEGF]

In DACD and DFGH, we have

ÐDAC = ÐHFG            [From (i)]

ÐACD = ÐFGH            [From (iv)]

DACD ~ DFGH            [By AA similarity]

Þ    \displaystyle \frac{CD}{GH}=\frac{AC}{FG}

(ii)

In DDCB and DHGE, we have

ÐDBC = ÐHEG            [From (ii)]

ÐDCB = ÐHGE            [From (v)]

\    DDCB ~ DHGE            [By AA similarity]

admin