CBSE 10th Mathematics | Similar Triangles | Introduction

Similar Triangles | Introduction

Similar figures: Geometric figures which have the same shape but different sizes are known as similar figures.

Illustrations:

1. Any two line-segments are similar

2. Any two squares are similar

3. Any two circles are similar

Two congruent figures are always similar but two similar figures need not be congruent.

Similar polygons: Two polygons of the same number of sides are said to be similar if

(i) Their corresponding angles are equal (i.e., they are equiangular) and

(ii) Their corresponding sides are in the same ratio (or proportion)

Similar triangles: Since triangles are also polygons, the same conditions of similarity are applicable to them.

Two triangles are said to be similar if

(i) Their corresponding angles are equal and

(ii) Their corresponding sides are in the same ratio (or proportion).

BASIC-PROPORTIONALITY THEOREM (Thales theorem)

Theorem: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

Given: A triangle ABC in which a line parallel to side BC intersects other two sides AB and AC at D and E respectively

To prove: $\displaystyle \frac{AD}{DB}=\frac{AE}{EC}.$

Construction: Join BE and CD and draw DM ^ AC and EN ^ AB.

Proof: area of DADE $\displaystyle (=\frac{1}{2}\text{base}\times \text{height})=\frac{1}{2}AD\times EN.$

(Taking AD as base)

So,

$\displaystyle \text{ar}(ADE)=\frac{1}{2}AD\times EN$ [The area of DADE is denoted as ar (ADE)]

Similarly,

$\displaystyle \text{ar}(BDE)=\frac{1}{2}DB\times EN,$

$\displaystyle \text{ar}(ADE)=\frac{1}{2}AE\times DM$ and $\displaystyle \text{ar}(DEC)=\frac{1}{2}EC\times DM.$

(Taking AE as base)

Therefore,

$\displaystyle \frac{\text{ar}(ADE)}{\text{ar(}BDE\text{)}}=\frac{\frac{1}{2}AD\times EN}{\frac{1}{2}DB\times EN}=\frac{AD}{DB}$ …(i)

and

$\displaystyle \frac{\text{ar}(ADE)}{\text{ar(}DEC\text{)}}=\frac{\frac{1}{2}AE\times DM}{\frac{1}{2}EC\times DM}=\frac{AE}{EC}$ …(ii)

$\displaystyle \text{ar}(BDE)=\text{ar}(DEC)$ … (iii)

DBDE and DEC are on the same base DE and between the same parallels BC and DE.]

Therefore, from (i), (ii) and (iii), we have: $\displaystyle \frac{AD}{DB}=\frac{AE}{EC}$

Corollary:

From above equation we have $\displaystyle \frac{DB}{AD}=\frac{EC}{AE}$

Adding ‘1’ to both sides we have

$\displaystyle \frac{DB}{AD}+1=\frac{EC}{AE}+1$

$\displaystyle \frac{DB+AD}{AD}=\frac{EC+AE}{AE}$ Þ $\displaystyle \frac{AB}{AD}=\frac{AC}{AE}$

Theorem: (Converse of BPT theorem) If a line divides any two sides of a triangle in the same ratio, prove that it is parallel to the third side.

Given:

In DABC, DE is a straight line such that $\displaystyle \frac{AD}{DB}=\frac{AE}{EC}$

To prove:

DE || BC

Construction:

If DE is not parallel to BC, draw DF meeting AC at F

Proof:

In DABC, let DF || BC

\ $\displaystyle \frac{AD}{DB}=\frac{AF}{FC}$ …(i)

[ $\displaystyle \because$ A line drawn parallel to one side of a D divides the other two sides in the same ratio.]

But $\displaystyle \frac{AD}{DB}=\frac{AE}{EC}$ …(ii) [given]

From (i) and (ii), we get

$\displaystyle \frac{AF}{FC}=\frac{AE}{EC}$

Adding 1 to both sides, we get

$\displaystyle \frac{AF}{FC}+1=\frac{AE}{EC}+1$

Þ $\displaystyle \frac{AF+FC}{FC}=\frac{AE+EC}{EC}$

Þ $\displaystyle \frac{AC}{FC}=\frac{AC}{EC}$ Þ
FC = EC

It is possible only when E and F coincide

Hence, DE || BC.

Question:

M and N are points on the sides PQ and PR respectively of DPQR. State whether MN II QR. Given PQ = 15.2 cm, PR = 12.8 cm, PM = 5.7 cm, PN = 4.8 cm.

Solution:

It has been given that

PQ = 15.2 cm, PR = 12.8 cm,

PM = 5.7 cm and PN = 4.8 cm

\ MQ = PQ – PM = (15.2 – 5.7) cm = 9.5 cm and

NR = PR – PN = (12.8 – 4.8) cm = 8 cm

Now

$\displaystyle \frac{PM}{MQ}=\frac{5.7}{9.5}=\frac{3}{5}$ and $\displaystyle \frac{PN}{NR}=\frac{4.8}{8}=\frac{3}{5}$

\ $\displaystyle \frac{PM}{MQ}=\frac{PN}{NR}$

Thus, in DPQR, MN divides the sides PQ and PR in the same ratio. Therefore, by the converse of the Basic Proportionality Theorem, we have MN II QR.

Question:

In the following figure, if AB II DC, find the value of x.

Solution:

Since the diagonals of a trapezium divide each other proportionally

\ $\displaystyle \frac{AO}{OC}=\frac{BO}{OD}$

Þ $\displaystyle \frac{7x-9}{2x-1}=\frac{9x-8}{3x}$

Þ $\displaystyle 21{{x}^{2}}-27x=18{{x}^{2}}-9x-16x+8$

Þ $\displaystyle 21{{x}^{2}}-27x=18{{x}^{2}}-25x+8$

Þ $\displaystyle 3{{x}^{2}}-2x-8=0$

Þ $\displaystyle 3{{x}^{2}}-6x+4x-8=0$

Þ 3x(x – 2) + 4 (x – 2) = 0

Þ $\displaystyle (x-2)\,(3x+4)=0$

Þ Either $\displaystyle x-2=0$ or $\displaystyle 3x+4=0$

Þ $\displaystyle x=2$ or $\displaystyle x=-\frac{4}{3}$

$\displaystyle [x=-\frac{4}{3},$ rejected, as it makes line-segments negative]

Thus, $\displaystyle x=2.$

Question:

In the given figure (i) and (ii) DE || BC. Find EC in (i) and AD in (ii)

Solution:

(i)

$\displaystyle \because$ In DABC, DE || BC then by Basic Proportionality (BPT) Theorem, we have

$\displaystyle \frac{AD}{DB}=\frac{AE}{EC}$ or cm

(ii)

Also in figure (ii), in DABC, DE || BC then by B.P.T, we have

$\displaystyle \frac{AD}{DB}=\frac{AE}{EC}$ or $\displaystyle AD=\frac{AE\times DB}{EC}=\frac{1.8\times 7.2}{5.4}$ = 2.4 cm

Question:

In the following figure, if LM || CB and LN || CD, prove that 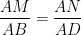$\displaystyle \frac{AM}{AB}=\frac{AN}{AD}$

Solution:

Given:

LM || CB and LN || CD

To prove:

$\displaystyle \frac{AM}{AB}=\frac{AN}{AD}$

Proof:

In DABC, LM || BC, then

By BPT Theorem, we have

$\displaystyle \frac{AM}{AB}=\frac{AL}{AC}$ …(i) [Corollary of B.P.T.]

Similarly, in DADC, LN || CD

$\displaystyle \frac{AN}{AD}=\frac{AL}{AC}$ …(ii) [Corollary of B.P.T.]

From (i) and (ii), we have $\displaystyle \frac{AM}{AB}=\frac{AN}{AD}$

Question:

In the figure, if DE || AC and DF || AE, prove that $\displaystyle \frac{BF}{EF}=\frac{BE}{CE}$ .

Solution:

In DABC, DE || AC then by B.P.T., we have

$\displaystyle \frac{BD}{DA}=\frac{BE}{EC}$ …(i)

In DABE, DF || AE then by B.P.T., we have

$\displaystyle \frac{BD}{DA}=\frac{BF}{EF}$ …(ii)

From (i) and (ii), we get

$\displaystyle \frac{BF}{EF}=\frac{BE}{CE}$

Question:

In the given figure, if DE || OQ and DF || OR, prove that EF || QR.

Solution:

In DPOQ, DE || OQ, then by BPT Theorem, we have

$\displaystyle \frac{PE}{EQ}=\frac{PD}{DO}$ …(i)

Also, in DPOR, DF || OR, then by BPT Theorem, we have

$\displaystyle \frac{PF}{FR}=\frac{PD}{DO}$ …(ii)

From equations, (i) and (ii),

$\displaystyle \frac{PE}{EQ}=\frac{PF}{FR}$

Þ $\displaystyle EF||QR$ [converse of BPT Theorem]

Question:

In figure, PQ || AB and PR || AC, prove that QR || BC.

Solution:

In DPOQ, PQ || AB, then by B.P.T., we have

$\displaystyle \frac{OP}{PA}=\frac{OQ}{QB}$ …(i)

Also in DPOR, AC || PR, we have

$\displaystyle \frac{OP}{PA}=\frac{OR}{RC}$ …(ii)

From (i) and (ii), we get

$\displaystyle \frac{OQ}{QB}=\frac{OR}{RC}$

Þ QR || BC [by converse of B.P.T.]

Question:

Using Basic proportionality theorem, prove that the line drawn through the mid point of one side of a triangle parallel to another side bisects the third side.

Solution:

Given: A DABC in which D is the mid point of AB and DE || BC meeting AC at E.

To prove:
AE = CE.

Proof: In DABC, DE || BC

\ $\displaystyle \frac{AD}{BD}=\frac{AE}{CE}$ [BPT Theorem]

But AD = BD [D is the mid point of AB]

\ $\displaystyle \frac{AE}{CE}=1$ Þ AE = CE

Hence, E is the mid point of AC.

Question:

ABCD is a trapezium such that AB || DC. The diagonals AC and BD intersect at O. Prove that 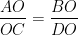$\displaystyle \frac{AO}{OC}=\frac{BO}{DO}$ or $\displaystyle \frac{AO}{BO}=\frac{CO}{DO}$ .

Solution:

Given:

ABCD is a trapezium such that AB || DC

To prove:

$\displaystyle \frac{AO}{OC}=\frac{BO}{DO}$ or $\displaystyle \frac{AO}{BO}=\frac{CO}{DO}$

Construction:

Through O draw OE || CD.

Proof:

AB || DC [given]

and EO || DC [const.]

Þ EO || AB

( $\displaystyle \because$ Two lines parallel to same line are parallel to each other)

Now, in DABD, EO || AB, then by BPT Theorem we have

$\displaystyle \frac{AE}{ED}=\frac{BO}{DO}$ …(i)

Also in DADC, EO || DC, by BPT Theorem, we have

$\displaystyle \frac{AE}{ED}=\frac{AO}{OC}$ …(ii)

From (i) and (ii), we get

$\displaystyle \frac{BO}{DO}=\frac{AO}{OC}$ or $\displaystyle \frac{AO}{BO}=\frac{CO}{DO}$

Question:

The diagonals of a quadrilateral ABCD intersect each other at the point O such that $\displaystyle \frac{AO}{BO}=\frac{CO}{DO}$ . Show that ABCD is a trapezium.

Solution:

Given:

A quadrilateral ABCD, whose diagonals AC and BD intersect at O such that

$\displaystyle \frac{AO}{BO}=\frac{CO}{DO}$ or $\displaystyle \frac{AO}{OC}=\frac{BO}{OD}$

To prove:

ABCD is a trapezium.

Construction:

Though O, draw a line OE parallel to AB intersecting BC at E.

Proof:

In DABC, OE || AB [By construction]

\ $\displaystyle \frac{AO}{OC}=\frac{BE}{EC}$ [by BPT Theorem] …(i)

$\displaystyle \frac{AO}{OC}=\frac{BO}{OD}$ [given] …(ii)

From (i) and (ii), we have $\displaystyle \frac{BO}{OD}=\frac{BE}{EC}$

Now, in DDBC, we have $\displaystyle \frac{BO}{OD}=\frac{BE}{EC}$

Þ OE || DC [Converse of BPT Theorem]

Now, in quadrilateral ABCD, OE || AB and OE || DC
Þ
AB || DC

( $\displaystyle \because$ Two lines parallel to same line are parallel to each other)

\ Quadrilateral ABCD is a trapezium.

CBSE Tutorials

CBSE 10th Mathematics | Similar Triangles | Introduction

Similar Triangles | Introduction

BASIC-PROPORTIONALITY THEOREM (Thales theorem)

Question:

M and N are points on the sides PQ and PR respectively of DPQR. State whether MN II QR. Given PQ = 15.2 cm, PR = 12.8 cm, PM = 5.7 cm, PN = 4.8 cm.

Solution:

Question:

In the following figure, if AB II DC, find the value of x.

Solution:

Question:

In the given figure (i) and (ii) DE || BC. Find EC in (i) and AD in (ii)

Solution:

Question:

In the following figure, if LM || CB and LN || CD, prove that $\displaystyle \frac{AM}{AB}=\frac{AN}{AD}$

Solution:

Question:

In the figure, if DE || AC and DF || AE, prove that $\displaystyle \frac{BF}{EF}=\frac{BE}{CE}$ .

Solution:

Question:

In the given figure, if DE || OQ and DF || OR, prove that EF || QR.

Solution:

Question:

In figure, PQ || AB and PR || AC, prove that QR || BC.

Solution:

Question:

Using Basic proportionality theorem, prove that the line drawn through the mid point of one side of a triangle parallel to another side bisects the third side.

Solution:

Question:

ABCD is a trapezium such that AB || DC. The diagonals AC and BD intersect at O. Prove that $\displaystyle \frac{AO}{OC}=\frac{BO}{DO}$ or $\displaystyle \frac{AO}{BO}=\frac{CO}{DO}$ .

Solution:

Question:

The diagonals of a quadrilateral ABCD intersect each other at the point O such that $\displaystyle \frac{AO}{BO}=\frac{CO}{DO}$ . Show that ABCD is a trapezium.

Solution:

Like this:

CBSE 10th Mathematics | Similar Triangles | Introduction

Similar Triangles | Introduction

BASIC-PROPORTIONALITY THEOREM (Thales theorem)

Question:

M and N are points on the sides PQ and PR respectively of DPQR. State whether MN II QR. Given PQ = 15.2 cm, PR = 12.8 cm, PM = 5.7 cm, PN = 4.8 cm.

Solution:

Question:

In the following figure, if AB II DC, find the value of x.

Solution:

Question:

In the given figure (i) and (ii) DE || BC. Find EC in (i) and AD in (ii)

Solution:

Question:

In the following figure, if LM || CB and LN || CD, prove that

Solution:

Question:

In the figure, if DE || AC and DF || AE, prove that .

Solution:

Question:

In the given figure, if DE || OQ and DF || OR, prove that EF || QR.

Solution:

Question:

In figure, PQ || AB and PR || AC, prove that QR || BC.

Solution:

Question:

Using Basic proportionality theorem, prove that the line drawn through the mid point of one side of a triangle parallel to another side bisects the third side.

Solution:

Question:

ABCD is a trapezium such that AB || DC. The diagonals AC and BD intersect at O. Prove that or .

Solution:

Question:

The diagonals of a quadrilateral ABCD intersect each other at the point O such that . Show that ABCD is a trapezium.

Solution:

Share this:

Like this:

In the following figure, if LM || CB and LN || CD, prove that $\displaystyle \frac{AM}{AB}=\frac{AN}{AD}$

In the figure, if DE || AC and DF || AE, prove that $\displaystyle \frac{BF}{EF}=\frac{BE}{CE}$ .

ABCD is a trapezium such that AB || DC. The diagonals AC and BD intersect at O. Prove that $\displaystyle \frac{AO}{OC}=\frac{BO}{DO}$ or $\displaystyle \frac{AO}{BO}=\frac{CO}{DO}$ .

The diagonals of a quadrilateral ABCD intersect each other at the point O such that $\displaystyle \frac{AO}{BO}=\frac{CO}{DO}$ . Show that ABCD is a trapezium.