CBSE 10th Mathematics | Triangles | Pythagoras Theorem

Triangles | Pythagoras Theorem

Theorem:

In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Given: A right triangle ABC, right angled at B

To prove:
$\displaystyle A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$

Construction: Draw BD ^ AC

Proof:
In DADB and DABC, we have

ÐADB = ÐABC [Each equal to 90°]

ÐA = ÐA [Common]

\
DADB ~ DABC [By AA similarity]

Þ $\displaystyle \frac{AD}{AB}=\frac{AB}{AC}$ [Corresponding sides of similar triangles are proportional]

Þ $\displaystyle A{{B}^{2}}=AD\times AC$ …(i)

In DBCD and DACB, we have

ÐCDB = ÐCBA [Each equal to 90°]

ÐC = ÐC [Common]

By AA similarity criterion

DBCD ~ DACB

\ $\displaystyle \frac{BC}{AC}=\frac{DC}{BC}$

Þ $\displaystyle B{{C}^{2}}=DC\times AC$ …(ii)

Adding equations (i) and (ii), we get

$\displaystyle A{{B}^{2}}+B{{C}^{2}}=AD\times AC+DC\times AC$

$\displaystyle =AC\,(AD+DC)=AC\times AC=A{{C}^{2}}$

Hence, $\displaystyle A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}.$

Theorem (Converse of Pythagoras theorem):

In a triangle if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.

Given: A triangle ABC such that $\displaystyle A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}.$

To prove:
$\displaystyle \angle B=90{}^\circ$

Construction: Draw a DPQR right angled at Q such that PQ = AB and QR = BC.

Proof: In right triangle PQR, we have

$\displaystyle P{{Q}^{2}}+Q{{R}^{2}}=P{{R}^{2}}$ [By Pythagoras Theorem]

Þ $\displaystyle A{{B}^{2}}+B{{C}^{2}}=P{{R}^{2}}$ …(i)

[ $\displaystyle \because$
PQ = AB and QR = BC (by construction)]

But $\displaystyle A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$ [Given] …(ii)

From equation (i) and equation (ii), we get

$\displaystyle P{{R}^{2}}=A{{C}^{2}}$

Þ $\displaystyle PR=AC$ …(iii)

Now, in DABC and DPQR, we have

AB = PQ and BC = QR [By construction]

and $\displaystyle AC=PR$ [From (iii)]

\ DABC @
DPQR [By SSS congruency]

\ ÐB = ÐQ = 90° [c.p.c.t.]

Hence, ÐB = 90°.

Solved Questions based on Pythagoras Theorem

Question:

The sides of some triangles are given below. Determine which of them are right triangles.

(i) 7 cm, 24 cm, 25 cm

(ii) 7 cm, 8 cm, 6 cm

Solution:

If the sum of the squares of the smaller sides of a triangle is equal to the square of the larger side, then the triangle is right angled.

(i)

(7 cm)² + (24 cm)² = (49 + 576) cm² = 625 cm² and (25 cm)² = 625 cm²

Hence, the given triangle is a right triangle.

(ii)

(7 cm)² + (6 cm)² = (49 + 36) cm² = 85 cm² and (8 cm)² = 64 cm²

Hence, the given triangle is not a right triangle.

Question:

A ladder is placed in such a way that its foot is at a distance of 5 m from a wall and its top reaches a window 12 m above the ground. Determine the length of the ladder.

Solution:

Let AB be the ladder, B be the window and BC be the wall

Then BC = 12 m, AC = 5m and ÐACB = 90°

In right triangle ACB, we have

$\displaystyle A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}$ [By Pythagoras Theorem]

Þ $\displaystyle A{{B}^{2}}={{(5)}^{2}}+{{(12\,)}^{2}}=(25+144)\,\,=169\,$

Þ $\displaystyle AB=13\,\text{m}$

Hence, the length of the ladder is 13 m.

Question:

A ladder 15 m long reaches a window which is 9 m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 12 m high. Find the width of the street.

Solution:

Let AB be the street and let C and D be the windows at heights of 9 m and 12 m respectively from the ground.

Let E be the foot of the ladder. Then EC and ED are the two positions of the ladder.

Clearly AC = 9 m, BD = 12 m, EC = ED = 15 m and ÐCAE = ÐDBE = 90°

In right triangle CAE, we have

$\displaystyle C{{E}^{2}}=A{{C}^{2}}+A{{E}^{2}}$ [By Pythagoras Theorem]

Þ (15)² = (9)² + AE²

Þ AE² = (15)² – (9)² = (225 – 81) = 144

Þ AE = 12 m …(i)

In right triangle DBE, we have

$\displaystyle D{{E}^{2}}=B{{D}^{2}}+E{{B}^{2}}$ [By Pythagoras Theorem]

Þ (15)² = (12)² + EB²

Þ EB² = (15)² – (12)² = (225 – 144) = 81

Þ EB = 9 m …(ii)

Adding equations (i) and (ii), we get

AE + EB = (12 + 9) m Þ AB = 21 m

Hence, the width of the street is 21 m.

Question:

In figure, ÐACB = 90° and CD
^
AB. Prove that 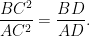$\displaystyle \frac{B{{C}^{2}}}{A{{C}^{2}}}=\frac{BD}{AD}.$

Solution:

Given:
ÐACB = 90° and CD ^ AB

To prove: $\displaystyle \frac{B{{C}^{2}}}{A{{C}^{2}}}=\frac{BD}{AD}.$

Proof: In DACD and DABC

ÐA = ÐA [Common]

ÐADC = ÐACB [Both 90°]

\ DACD ~ DABC [By AA similarity]

So, $\displaystyle \frac{AC}{AB}=\frac{AD}{AC}$

or, $\displaystyle A{{C}^{2}}=AB.AD$ …(i)

Similarly, DBCD ~ DBAC

So, $\displaystyle \frac{BC}{BA}=\frac{BD}{BC}$

or, $\displaystyle B{{C}^{2}}=BA.BD$ …(ii)

Therefore, from (i) and (ii),

$\displaystyle \frac{B{{C}^{2}}}{A{{C}^{2}}}=\frac{BA.BD}{AB.AD}=\frac{BD}{AD}$

Question:

P and Q are the midpoints of the sides CA and CB respectively of DABC, right angled at C. Prove that

(i) 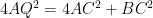$\displaystyle 4A{{Q}^{2}}=4A{{C}^{2}}+B{{C}^{2}}$

(ii) $\displaystyle 4B{{P}^{2}}=4B{{C}^{2}}+A{{C}^{2}}$

(iii) $\displaystyle 4(A{{Q}^{2}}+B{{P}^{2}})=5A{{B}^{2}}$

Solution:

Given: P and Q are the midpoints of the sides CA and CB respectively of DABC, right angled at C

To Prove:

(i) $\displaystyle 4A{{Q}^{2}}=4A{{C}^{2}}+B{{C}^{2}}$

(ii) $\displaystyle 4B{{P}^{2}}=4B{{C}^{2}}+A{{C}^{2}}$

(iii) $\displaystyle 4(A{{Q}^{2}}+B{{P}^{2}})=5A{{B}^{2}}$

Proof:

(i)

From right DACQ, we have

$\displaystyle A{{Q}^{2}}=A{{C}^{2}}+Q{{C}^{2}}$ [By Pythagoras Theorem]

Þ $\displaystyle A{{Q}^{2}}=A{{C}^{2}}+{{\left( \frac{BC}{2} \right)}^{2}}$ [ $\displaystyle \because$ Q is the midpoint of CB]

Þ $\displaystyle A{{Q}^{2}}=A{{C}^{2}}+\frac{B{{C}^{2}}}{4}$

Þ $\displaystyle 4A{{Q}^{2}}=4A{{C}^{2}}+B{{C}^{2}}$ …(i)

(ii)

From right DBCP

$\displaystyle B{{P}^{2}}=B{{C}^{2}}+P{{C}^{2}}$ [By Pythagoras Theorem]

Þ $\displaystyle B{{P}^{2}}=B{{C}^{2}}+{{\left( \frac{AC}{2} \right)}^{2}}$ [ $\displaystyle \because$ P is the mid-point of side CA]

Þ $\displaystyle B{{P}^{2}}=B{{C}^{2}}+\frac{A{{C}^{2}}}{4}$

Þ $\displaystyle 4B{{P}^{2}}=4B{{C}^{2}}+A{{C}^{2}}$ … (ii)

(iii)

Adding equation (i) and equation (ii), we get

$\displaystyle 4(A{{Q}^{2}}+B{{P}^{2}})=4(A{{C}^{2}}+B{{C}^{2}})+(B{{C}^{2}}+A{{C}^{2}})$

Þ $\displaystyle 4(A{{Q}^{2}}+B{{P}^{2}})=5\,(A{{C}^{2}}+B{{C}^{2}})$

Þ $\displaystyle 4(A{{Q}^{2}}+B{{P}^{2}})=5\,A{{B}^{2}}$ [ $\displaystyle \because$ In DABC, $\displaystyle A{{C}^{2}}+B{{C}^{2}}=A{{B}^{2}}$ ]

Hence, $\displaystyle 4(A{{Q}^{2}}+B{{P}^{2}})=5\,\,A{{B}^{2}}.$

Question:

O is any point inside a rectangle ABCD in figure. Prove that OB² + OD² = OA² + OC².

Solution:

Given: O is any point inside a rectangle ABCD

To prove:
OB² + OD² = OA² + OC²

Construction:
Through O, draw PQ || BC so that P lies on AB and Q lies on DC.

Proof: PQ || BC [By construction]

Therefore, PQ ^ AB and PQ ^ DC (ÐB = 90° and ÐC = 90°)

So, ÐBPQ = 90° and ÐCQP = 90°

Therefore, BPQC and APQD are both rectangles.

Now, from DOPB,

$\displaystyle O{{B}^{2}}=B{{P}^{2}}+O{{P}^{2}}$ …(i)

Similarly, from DOQD,

$\displaystyle O{{D}^{2}}=O{{Q}^{2}}+D{{Q}^{2}}$ …(ii)

From DOQC, we have

$\displaystyle O{{C}^{2}}=O{{Q}^{2}}+C{{Q}^{2}}$ …(iii)

and from DOAP, we have

$\displaystyle O{{A}^{2}}=A{{P}^{2}}+O{{P}^{2}}$ …(iv)

Adding (i) and (ii),

$\displaystyle O{{B}^{2}}+O{{D}^{2}}=B{{P}^{2}}+O{{P}^{2}}+O{{Q}^{2}}+D{{Q}^{2}}$

$\displaystyle =C{{Q}^{2}}+O{{P}^{2}}+O{{Q}^{2}}+A{{P}^{2}}$

(As BP = CQ and DQ = AP)

$\displaystyle =\left( C{{Q}^{2}}+O{{Q}^{2}} \right)+\left( O{{P}^{2}}+A{{P}^{2}} \right)$

$\displaystyle =O{{C}^{2}}+O{{A}^{2}}$ [From (iii) and (iv)]

Question:

ABC is a triangle right-angled at C and p is the length of the perpendicular from C to AB. Show that

(a) pc = ab

(b) 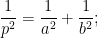$\displaystyle \frac{1}{{{p}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}};$ where a = BC, b = AC and c = AB.

Solution:

(a)

Taking c as the base and p as the altitude, we have

area of DABC
$\displaystyle =\frac{1}{2}pc$ …(i)

Taking b as the base and a as the altitude, we have

area DABC = $\displaystyle \frac{1}{2}ab$ …(ii)

\ $\displaystyle \frac{1}{2}pc=\frac{1}{2}ab$ [From (i) and (ii)]

Þ pc = ab Hence Proved.

(b)

$\displaystyle \because$
ABC is a right triangle-angled at C.

\ $\displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}$ …(iii)

[By Pythagoras Theorem]

pc = ab [proved above]

\ $\displaystyle p=\frac{ab}{c}$

or $\displaystyle \frac{1}{p}=\frac{c}{ab}$

Þ $\displaystyle \frac{1}{{{p}^{2}}}=\frac{{{c}^{2}}}{{{a}^{2}}{{b}^{2}}}=\frac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}{{b}^{2}}}$ [From equation (iii)]

$\displaystyle =\frac{{{a}^{2}}}{{{a}^{2}}{{b}^{2}}}+\frac{{{b}^{2}}}{{{a}^{2}}{{b}^{2}}}=\frac{1}{{{b}^{2}}}+\frac{1}{{{a}^{2}}}.$

Þ $\displaystyle \frac{1}{{{p}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}.$

Question:

In DABC, ÐC > 90° and side AC is produced to D such that segment BD is perpendicular to segment AD. Prove that $\displaystyle A{{B}^{2}}=A{{C}^{2}}+2CA\times CD.$

Solution:

Given:
DABC in which ÐACB > 90°.

To prove: $\displaystyle A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}+2CA\times CD.$

Construction: Draw BD ^ AC (produced).

Proof: In right-triangle DBDA, we get

$\displaystyle A{{B}^{2}}=B{{D}^{2}}+A{{D}^{2}}$ …(i) [By Pythagoras theorem]

$\displaystyle =B{{D}^{2}}+{{(AC+CD)}^{2}}$ [ $\displaystyle \because$ AD = AC + CD]

$\displaystyle =B{{D}^{2}}+A{{C}^{2}}+C{{D}^{2}}+2AC.CD$

$\displaystyle =(B{{D}^{2}}+C{{D}^{2}})+A{{C}^{2}}+2AC.CD$

[ $\displaystyle \because$ In right-angled DBDC, BD² + CD² = BC²] [By Pythagoras theorem]

$\displaystyle =B{{C}^{2}}+A{{C}^{2}}+2AC.CD$

Hence, $\displaystyle A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}+2CA\times CD.$

Question:

In DABC, ÐB < 90° and AD is drawn perpendicular to BC. Prove that 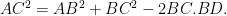$\displaystyle A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2BC.BD.$

Solution:

Given:
DABC in which ÐB < 90° and AD is perpendicular to BC

To prove: $\displaystyle A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2BC.BD.$

Proof: In right-angled DABD, we have

$\displaystyle A{{D}^{2}}+B{{D}^{2}}=A{{B}^{2}}$ [By Pythagoras theorem]…(i)

In right-angled DADC, we have

$\displaystyle A{{C}^{2}}=A{{D}^{2}}+D{{C}^{2}}$

$\displaystyle =A{{D}^{2}}+{{(BC-BD)}^{2}}$ [ $\displaystyle \because$ DC = BC – BD]

$\displaystyle =A{{D}^{2}}+B{{C}^{2}}+B{{D}^{2}}-2BC.BD$

$\displaystyle =(A{{D}^{2}}+B{{D}^{2}})+B{{C}^{2}}-2BC.BD$ [ $\displaystyle \because$ In D
ABD, AB²= AD² + BD²]

$\displaystyle =A{{B}^{2}}+B{{C}^{2}}-2BC.BD.$

Þ $\displaystyle A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2BC.BD.$

Question:

The perpendicular from A on the side BC of a DABC intersects BC at D such that DB = 3 CD. Prove that 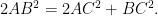$\displaystyle 2A{{B}^{2}}=2A{{C}^{2}}+B{{C}^{2}}.$

Solution:

Given: In DABC, AD ^ BC and BD = 3 CD.

To prove: $\displaystyle 2A{{B}^{2}}=2A{{C}^{2}}+B{{C}^{2}}$

Proof: $\displaystyle BD=3CD\,$ (given)

Adding CD on both sides

$\displaystyle BD+DC=4CD$

BC = 4CD

$\displaystyle \therefore CD=\frac{BC}{4}$ …(i)

In DABD, we have,

$\displaystyle A{{B}^{2}}=B{{D}^{2}}+A{{D}^{2}}$ [Pythagoras Theorem]

$\displaystyle =A{{D}^{2}}+{{(BC-DC)}^{2}}$

Þ $\displaystyle A{{B}^{2}}=A{{D}^{2}}+B{{C}^{2}}+D{{C}^{2}}-2BC.CD$

$\displaystyle =B{{C}^{2}}+(A{{D}^{2}}+D{{C}^{2}})-2BC.CD$

$\displaystyle =B{{C}^{2}}+A{{C}^{2}}-2BC.CD$

[ $\displaystyle \because$ In DADC, $\displaystyle A{{C}^{2}}=A{{D}^{2}}+C{{D}^{2}}$ ]

$\displaystyle =B{{C}^{2}}+A{{C}^{2}}-\frac{2BC\times BC}{4}$ [From (i)]

$\displaystyle =B{{C}^{2}}+A{{C}^{2}}-\frac{B{{C}^{2}}}{2}$

Þ $\displaystyle A{{B}^{2}}=A{{C}^{2}}+\frac{B{{C}^{2}}}{2}$

or $\displaystyle 2A{{B}^{2}}=2A{{C}^{2}}+B{{C}^{2}}$

Question:

In an equilateral triangle ABC, D is a point on BC such that 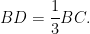$\displaystyle BD=\frac{1}{3}BC.$ Prove that $\displaystyle 9A{{D}^{2}}=7A{{B}^{2}}.$

Solution:

Given: In DABC is an equilateral triangle and D is a point on BC such that $\displaystyle BD=\frac{1}{3}BC.$

To prove: $\displaystyle 9A{{D}^{2}}=7A{{B}^{2}}$

Construction: Draw $\displaystyle AE\bot BC$ and join A to D.

Proof: In DAEB and DAEC, we have

$\displaystyle AE=AE$ [Common]

ÐAEB = ÐAEC [Each = 90°]

$\displaystyle AB=AC$ [ABC is an equilateral triangle]

\ DAEB @ DAEC [R.H.S. congruency]

\ BE = EC [c.p.c.t.]

Now, $\displaystyle BD=\frac{1}{3}BC$ and $\displaystyle BE=EC=\frac{1}{2}BC.$

In DABE

$\displaystyle A{{B}^{2}}=A{{E}^{2}}+B{{E}^{2}}$ [By Pythagoras theorem]

$\displaystyle A{{B}^{2}}$ $\displaystyle =A{{E}^{2}}+{{\left( BD+DE \right)}^{2}}$

$\displaystyle A{{B}^{2}}$ = $\displaystyle A{{E}^{2}}+B{{D}^{2}}+D{{E}^{2}}+2BD.DE$

$\displaystyle A{{B}^{2}}$ = $\displaystyle A{{D}^{2}}+B{{D}^{2}}+2\,BD.DE$ [ $\displaystyle \because$ In DADE
$\displaystyle A{{E}^{2}}+O{{E}^{2}}=A{{D}^{2}}$ ]

$\displaystyle A{{B}^{2}}$ $\displaystyle =A{{D}^{2}}+{{\left[ \frac{1}{3}BC \right]}^{2}}+2\times \frac{1}{3}BC\left[ BE-BD \right]$ [ $\displaystyle \because BD=\frac{1}{3}BC$ ]

$\displaystyle A{{B}^{2}}$ $\displaystyle =A{{D}^{2}}+\frac{1}{9}A{{B}^{2}}+\frac{2}{3}AB\left[ \frac{1}{2}AB-\frac{1}{3}AB \right]$ [ $\displaystyle \because AB=BC$ and $\displaystyle BE=\frac{1}{2}BC$ ]

$\displaystyle A{{B}^{2}}$ $\displaystyle =A{{D}^{2}}+\frac{1}{9}A{{B}^{2}}+\frac{2}{3}AB\left[ \frac{AB}{6} \right]$

$\displaystyle A{{B}^{2}}=A{{D}^{2}}+\frac{A{{B}^{2}}}{9}+\frac{A{{B}^{2}}}{9}$

$\displaystyle 9A{{B}^{2}}=9A{{D}^{2}}+2\,A{{B}^{2}}$

$\displaystyle 7A{{B}^{2}}=9A{{D}^{2}}$

Question:

Prove that three times the square of any side of an equilateral-triangle is equal to four times the square of the altitude.

Solution:

Given:
ABC be an equilateral triangle and let AD ^ BC.

To prove: 3AB² = 4AD²

Proof:
In DADB and DADC, we have

AB = AC [Given]

ÐB = ÐC [Each equal to 60°]

and, ÐADB = ÐADC [Each equal to 90°]

\ DADB @ DADC [By AAS congruency]

Þ BD = DC [c.p.c.t.]

Þ $\displaystyle BD=DC=\frac{1}{2}BC$

Since DADB is a right triangle right-angled at D.

\ $\displaystyle A{{B}^{2}}=A{{D}^{2}}+B{{D}^{2}}$

Þ $\displaystyle A{{B}^{2}}=A{{D}^{2}}+{{\left( \frac{1}{2}BC \right)}^{2}}$

Þ $\displaystyle A{{B}^{2}}=A{{D}^{2}}+\frac{B{{C}^{2}}}{4}$ [ $\displaystyle \because$
BC = AB]

Þ $\displaystyle 4A{{B}^{2}}=4A{{D}^{2}}+A{{B}^{2}}$ [ $\displaystyle \because$
BC = AB]

Þ $\displaystyle 4A{{B}^{2}}-A{{B}^{2}}=4A{{D}^{2}}$

Þ $\displaystyle 3A{{B}^{2}}=4A{{D}^{2}}$

Question:

ABC is a right triangle right-angled at C and 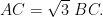$\displaystyle AC=\sqrt{3}\,\,BC.$ Prove that ÐABC = 60°.

Solution:

Given:
ABC is a right triangle right-angled at C and $\displaystyle AC=\sqrt{3}\,\,BC.$

To prove:
ÐABC = 60°

Construction: Let D be the mid-point of AB. Join CD.

Proof:
ABC is a right triangle right-angled at C.

\ $\displaystyle A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}$ [By Pythagoras theorem]

Þ $\displaystyle A{{B}^{2}}={{(\sqrt{3}BC)}^{2}}+B{{C}^{2}}$ [ $\displaystyle \because$
$\displaystyle AC=\sqrt{3}BC$ (Given)]

$\displaystyle A{{B}^{2}}=4B{{C}^{2}}$

Þ $\displaystyle AB=2BC$

But, $\displaystyle BD=\frac{1}{2}AB$ i.e., AB = 2BD

\ BD = BC

But mid-point of the hypotenuse of a right triangle is equidistant from the vertices.

\ CD = AD = BD

Þ CD = BC [ $\displaystyle \because$ BD = BC]

Thus, in DBCD, we have

BD = CD = BC

Þ DBCD is equilateral Þ ÐABC = 60°

Question:

The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.

Solution:

Given: A DABC in which AD is the internal bisector of ÐA and meets BC in D.

To Prove: $\displaystyle \frac{BD}{DC}=\frac{AB}{AC}$

Construction: Draw CE || DA to meet BA produced at E.

Proof: Ð2 = Ð3 …(i)

[Alternate angles]

and, Ð1 = Ð4 …(ii)

[Corresponding angles]

But, Ð1 = Ð2 [ $\displaystyle \because$
AD is the bisector of ÐA]

From (i) and (ii), we get

Ð3 = Ð4

Þ AE = AC …(iii)

[Sides opposite to equal angles are equal]

Now, in DBCE, we have

$\displaystyle DA||CE$ [By construction]

Þ $\displaystyle \frac{BD}{DC}=\frac{BA}{AE}$ [Using Basic Proportionality Theorem]

Þ $\displaystyle \frac{BD}{DC}=\frac{AB}{AC}$ [(From (iii)]

Hence, $\displaystyle \frac{BD}{DC}=\frac{AB}{AC}$

Question:

ABCD is a quadrilateral in which AB = AD. The bisector of ÐBAC and ÐCAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.

Solution:

Given: A quadrilateral ABCD in which AB = AD and the bisectors of ÐBAC and ÐCAD meet the sides BC and CD at E and F respectively.

To Prove:
EF || BD

Construction: Join AC, BD and EF.

Proof: In DCAB, AE is the bisector of ÐBAC.

\ $\displaystyle \frac{AC}{AB}=\frac{CE}{BE}$ …(i)

In DACD, AF is the bisector of ÐCAD.

\ $\displaystyle \frac{AC}{AD}=\frac{CF}{DF}$

Þ $\displaystyle \frac{AC}{AB}=\frac{CF}{DF}$ [ $\displaystyle \because$
AD = AB] …(ii)

From (i) and (ii), we get

$\displaystyle \frac{CE}{BE}=\frac{CF}{DF}$

Þ $\displaystyle \frac{CE}{EB}=\frac{CF}{FD}$

Therefore, by the converse of BPT Theorem, we have

EF || BD.

Question:

Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out in figure? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Solution:

(i)

In right angled DABC, AB = 1.8 cm, BC = 2.4 cm

\ $\displaystyle A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$

$\displaystyle A{{C}^{2}}={{(1.8)}^{2}}+{{(2.4)}^{2}}=3.24+5.76=9$ Þ $\displaystyle AC=\sqrt{9}=3\,\text{m}$

Hence the original length of the string AC is 3 m.

(ii)

When Nazima pulls in the string at the rate of 5 cm/sec, then the length of the string decreases = 5 ´ 12 cm = 60 cm = 0.60 m in 12 seconds.

\ Remaining length of the string (AD) after 12 seconds = (3 – 0.60) = 2.40 m

Now in right angled DABD,

$\displaystyle A{{D}^{2}}=D{{B}^{2}}+A{{B}^{2}}$

Þ
$\displaystyle D{{B}^{2}}=A{{D}^{2}}-A{{B}^{2}}={{(2.40)}^{2}}-{{(1.80)}^{2}}=2.52$ m Þ
$\displaystyle DB=\sqrt{2.52}\text{m}$ = 1.587 m

Þ Horizontal distance (DE) of the fly from Nazima

= (1.587 + 1.2) m = 2.787 m = 2.79 m.

CBSE 10th Mathematics | Triangles | Pythagoras Theorem

Triangles | Pythagoras Theorem

Solved Questions based on Pythagoras Theorem

Question:

The sides of some triangles are given below. Determine which of them are right triangles.

(i) 7 cm, 24 cm, 25 cm

(ii) 7 cm, 8 cm, 6 cm

Solution:

Question:

A ladder is placed in such a way that its foot is at a distance of 5 m from a wall and its top reaches a window 12 m above the ground. Determine the length of the ladder.

Solution:

Question:

A ladder 15 m long reaches a window which is 9 m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 12 m high. Find the width of the street.

Solution:

Question:

In figure, ÐACB = 90° and CD ^ AB. Prove that

Solution:

Question:

P and Q are the midpoints of the sides CA and CB respectively of DABC, right angled at C. Prove that

(i)

(ii)

(iii)

Solution:

Question:

O is any point inside a rectangle ABCD in figure. Prove that OB2 + OD2 = OA2 + OC2.

Solution:

Question:

ABC is a triangle right-angled at C and p is the length of the perpendicular from C to AB. Show that

(a) pc = ab

(b) where a = BC, b = AC and c = AB.

Solution:

Question:

In DABC, ÐC > 90° and side AC is produced to D such that segment BD is perpendicular to segment AD. Prove that

Solution:

Question:

In DABC, ÐB < 90° and AD is drawn perpendicular to BC. Prove that

Solution:

Question:

The perpendicular from A on the side BC of a DABC intersects BC at D such that DB = 3 CD. Prove that

Solution:

Question:

In an equilateral triangle ABC, D is a point on BC such that Prove that

Solution:

Question:

Prove that three times the square of any side of an equilateral-triangle is equal to four times the square of the altitude.

Solution:

Question:

ABC is a right triangle right-angled at C and Prove that ÐABC = 60°.

Solution:

Question:

The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.

Solution:

Question:

ABCD is a quadrilateral in which AB = AD. The bisector of ÐBAC and ÐCAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.

Solution:

Question:

Solution:

Share this:

Like this:

In figure, ÐACB = 90° and CD
^
AB. Prove that $\displaystyle \frac{B{{C}^{2}}}{A{{C}^{2}}}=\frac{BD}{AD}.$

(i) $\displaystyle 4A{{Q}^{2}}=4A{{C}^{2}}+B{{C}^{2}}$

(ii) $\displaystyle 4B{{P}^{2}}=4B{{C}^{2}}+A{{C}^{2}}$

(iii) $\displaystyle 4(A{{Q}^{2}}+B{{P}^{2}})=5A{{B}^{2}}$

O is any point inside a rectangle ABCD in figure. Prove that OB² + OD² = OA² + OC².

(b) $\displaystyle \frac{1}{{{p}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}};$ where a = BC, b = AC and c = AB.

In DABC, ÐC > 90° and side AC is produced to D such that segment BD is perpendicular to segment AD. Prove that $\displaystyle A{{B}^{2}}=A{{C}^{2}}+2CA\times CD.$

In DABC, ÐB < 90° and AD is drawn perpendicular to BC. Prove that $\displaystyle A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2BC.BD.$

The perpendicular from A on the side BC of a DABC intersects BC at D such that DB = 3 CD. Prove that $\displaystyle 2A{{B}^{2}}=2A{{C}^{2}}+B{{C}^{2}}.$

In an equilateral triangle ABC, D is a point on BC such that $\displaystyle BD=\frac{1}{3}BC.$ Prove that $\displaystyle 9A{{D}^{2}}=7A{{B}^{2}}.$

ABC is a right triangle right-angled at C and $\displaystyle AC=\sqrt{3}\,\,BC.$ Prove that ÐABC = 60°.