CBSE Tutorials

CBSE 10th Mathematics | Relation Between The Zeros And The Coefficients Of A Polynomial

Relation Between The Zeros And The Coefficients Of A Polynomial

 

1.    Quadratic polynomial: 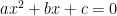\displaystyle a{{x}^{2}}+bx+c=0;     a ¹ 0.

    Let a, b are two zeros of the given polynomial.

    Sum of zeros (a + b) = \displaystyle -\frac{\text{coefficient}\,\text{of}\,\,x}{\text{coefficient}\,\text{of}\,\,{{x}^{2}}}=-\frac{b}{a}    

    Product of zeros (ab) = \displaystyle \frac{constant}{coefficient\,of\,\,{{x}^{2}}}=\frac{c}{a}    

2.    Cubic polynomial: \displaystyle a{{x}^{3}}+b{{x}^{2}}+cx+d=0; a ¹ 0

    Let a, b and g are three zeros of the given polynomial.

    (i) Sum of zeros \displaystyle (\alpha +\beta +\gamma )=-\frac{\text{coefficient of }{{x}^{\text{2}}}}{coefficient\,of\,\,{{x}^{3}}}=-\frac{b}{a}    

    (ii) Product of zeros taken two at a time

            (ab + bg + ga) = \displaystyle \frac{\text{coefficient of }x}{\text{coefficient of }{{x}^{\text{3}}}}=\frac{c}{a}

    (iii) Product of zeros (abg) = \displaystyle -\frac{\text{constant}}{\text{coefficient of }{{x}^{\text{3}}}}=-\frac{d}{a}

3.    Formation of Quadratic Polynomial:

    Let a, b are the zeros, then required polynomial is

        k[x2 – (sum of roots)x + (product of roots)] or k[(x–a)(x–b)]

                                where k is a non-zero constant

4.    Formation of Cubic Polynomial

    Let a, b, g are the zeros then required polynomial is

        \displaystyle k[{{x}^{3}}-(\alpha +\beta +\gamma ){{x}^{2}}+(\alpha \beta +\beta \gamma +\gamma \alpha )x-\alpha \beta \gamma ]     or \displaystyle k[(x-\alpha )(x-\beta )(x-\gamma )]

where k is a non-zero constant

 

 

Question:

 

Find the zeros of the following quadratic polynomials and verify the relationship between the zeros and their coefficients.

        (i) \displaystyle {{x}^{2}}-2x-8    (ii) \displaystyle 6{{x}^{2}}-3        (iii) \displaystyle 4{{u}^{2}}+8u

 

Solution:

 

(i)    Given quadratic polynomial is \displaystyle y={{x}^{2}}-2x-8={{x}^{2}}-4x+2x-8

             = \displaystyle x(x-4)+2(x-4)=(x+2)(x-4)

             = \displaystyle (x+2)(x-4)

            y = 0 gives x = –2, 4. These are two zeros such that a = –2, b = 4.

            \    Sum of zeros (a + b) = –2 + 4 = 2 = \displaystyle -\frac{(-2)}{1}=-\frac{b}{a}

            Product of zeros (ab) = – 2 × 4 = – 8 = \displaystyle -\frac{8}{1} = \displaystyle \frac{c}{a}

 

(ii)    Given quadratic polynomial is \displaystyle 6{{x}^{2}}-3

            y = \displaystyle 6{{x}^{2}}-3=3(2{{x}^{2}}-1)=3[{{(\sqrt{2}x)}^{2}}-{{(1)}^{2}}]=3(\sqrt{2}x+1)(\sqrt{2}x-1)

            y = 0 gives\displaystyle x=-\frac{1}{\sqrt{2}},\,\,\frac{1}{\sqrt{2}}. These are two zeros such that \displaystyle \alpha =-\frac{1}{\sqrt{2}},\,\,\beta =\frac{1}{\sqrt{2}}

            Sum of zeros (a + b) = \displaystyle -\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=0=-\frac{0}{6}=-\frac{b}{a}

            Product of zeros (ab) = \displaystyle -\frac{1}{\sqrt{2}}\times \frac{1}{\sqrt{2}}=-\frac{1}{2}=\frac{-3}{6} = \displaystyle \frac{c}{a}

 

(iii)    \displaystyle y=4{{u}^{2}}+8u=4u(u+2)

            y = 0 gives \displaystyle 4u=0 and \displaystyle u+2=0; i.e. u = 0, –2.

            a =0, b = –2

            Sum of zeros (a + b) = 0 – 2 = –2 = \displaystyle -\frac{8}{4} = \displaystyle -\frac{b}{a}

            Product of zeros (ab) = 0 × (–2) = \displaystyle \frac{0}{4}=\frac{c}{a}.

 

Question:

 

Find a quadratic polynomial, the sum and product of whose zeros are \displaystyle \frac{1}{2} and –1 respectively.

 

Solution:

 

Here \displaystyle \alpha +\beta =\frac{1}{2}, ab = –1

        \    Required polynomial is

        \displaystyle f(x)=k[{{x}^{2}}-(\alpha +\beta )x+(\alpha \beta )]

         =\displaystyle k\left( {{x}^{2}}-\frac{1}{2}x-1 \right) where k is a non-zero constant.

 

Question:

 

Form a cubic polynomial with zeros a = 3, b = 2, g = –1 .

 

Solution:

 

a = 3, b = 2, g = –1

        Required polynomial     = \displaystyle k[(x-\alpha )(x-\beta )(x-\gamma )]

                    = \displaystyle k[(x-3)(x-2)(x+1)]

                    = \displaystyle k[({{x}^{2}}-5x+6)(x+1)]

                    = \displaystyle k[{{x}^{3}}-5{{x}^{2}}+6x+{{x}^{2}}-5x+6]

                    = \displaystyle k[{{x}^{3}}-4{{x}^{2}}+x+6]

                        where k is a non-zero constant.

 

Question:

 

Find a quadratic polynomial whose zeros are 2 and –3.

 

Solution:

 

Required polynomial

        \displaystyle =k[(x-2)\,[x-(-3)]

        \displaystyle =k[(x-2)\,(x+3)]

        \displaystyle =k({{x}^{2}}+x-6)    

                    where k is a non-zero constant

 

Question:

 

If a and b are the zeros of the polynomial \displaystyle f(x)={{x}^{2}}-5x+k such that
a – b = 1, find the value of k.

 

Solution:

 

Since a and b are the zeros of the polynomial \displaystyle f(x)={{x}^{2}}-5x+k.

    \    \displaystyle \alpha +\beta =-\left( \frac{-5}{1} \right)=5 and \displaystyle \alpha \beta =\frac{k}{1}=k

    Now,    \displaystyle \alpha -\beta =1                    [Given]

    Þ    \displaystyle {{(\alpha -\beta )}^{2}}=1        

    Þ    \displaystyle {{(\alpha +\beta )}^{2}}-4\alpha \beta =1    \displaystyle [{{(\alpha -\beta )}^{2}}={{\alpha }^{2}}+{{\beta }^{2}}-2\alpha \beta ={{\alpha }^{2}}+{{\beta }^{2}}+2\alpha \beta -4\alpha \beta ]    

    Þ    25 – 4k = 1    

    Þ    24 = 4k

    Þ    k = 6

    Hence, the value of k is 6.

 

Question:

 

Verify that the numbers given alongside of the cubic polynomials below are the zeros. Also verify the relationship between the zeros and co-efficients in each case.

            \displaystyle {{x}^{3}}-4{{x}^{2}}+5x-2; 2, 1, 1

 

Solution:

 

Let \displaystyle P(x)={{x}^{3}}-4{{x}^{2}}+5x-2

        On comparing with \displaystyle a{{x}^{3}}+b{{x}^{2}}+cx+d

        \displaystyle a=1, \displaystyle b=-4, c = 5, d = –2

        Given zeros are 2, 1, 1.

        \displaystyle P(2)={{(2)}^{3}}-4{{(2)}^{2}}+5(2)-2=8-16+10-2=0

        \displaystyle P(1)={{1}^{3}}-4{{(1)}^{2}}+5(1)-2=1-4+5-2=0

        \    2, 1, 1 are zeros of \displaystyle P(x)

        a = 2, b = 1, g = 1

        \displaystyle \alpha +\beta +\gamma =2+1+1=4=-\frac{(-4)}{1}=-\frac{b}{a}

        \displaystyle \alpha \beta \gamma =2\times 1\times 1= \displaystyle -\frac{(-2)}{1} = \displaystyle -\frac{d}{a}    

        \displaystyle \alpha \beta +\beta \gamma +\gamma \alpha =2\times 1+1\times 1+1\times 2 = 2 + 1 +2 = \displaystyle 5=\frac{5}{1} = \displaystyle \frac{c}{a}

        Hence the result.

 

Question:

 

Write a rational expression whose numerator is a quadratic polynomial with zeros 2 and –1 and denominator is a quadratic polynomial with zeros \displaystyle \frac{1}{2} and 3.

 

Solution:

 

Zeros of numerator are 2 and –1.

        a = 2, b = –1, \displaystyle \alpha +\beta =2-1=1, \displaystyle \alpha \beta =2\times (-1)=-2

        Numerator is \displaystyle k[{{x}^{2}}-(1)x+(-2)]=k({{x}^{2}}-x-2)

        Zeros of denominator are \displaystyle \frac{1}{2}, 3.

        \displaystyle \alpha =\frac{1}{2}, \displaystyle \beta =3, \displaystyle \alpha +\beta =\frac{1}{2}+3=\frac{7}{2}, \displaystyle \alpha \beta =\frac{1}{2}\times 3=\frac{3}{2}

        Denominator is \displaystyle k\prime \,\left[ {{x}^{2}}-\frac{7}{2}x+\frac{3}{2} \right]=\frac{k\prime }{2}\left[ 2{{x}^{2}}-7x+3 \right]

                = \displaystyle k[2{{x}^{2}}-7x+3]    where k = \displaystyle \frac{k\prime }{2}.

        \    Rational expression is = \displaystyle \frac{\text{Numerator}}{Denominator}=\frac{{{x}^{2}}-x-2}{2{{x}^{2}}-7x+3}

                

Question:

 

Find a quadratic polynomial whose zeros are reciprocals of the zeros of the polynomial \displaystyle f(x)=a{{x}^{2}}+bx+c,\,\,a\ne 0,\,\,c\ne 0.

 

Solution:

 

Let a, b be the zeros of the polynomial \displaystyle f(x)=a{{x}^{2}}+bx+c. Then,

        \displaystyle \alpha +\beta =-\frac{b}{a} and \displaystyle \alpha \beta =\frac{c}{a}

    Let S and P denote respectively the sum and product of the zeros of a polynomial whose zeros are \displaystyle \frac{1}{\alpha } and \displaystyle \frac{1}{\beta }. Then,

        \displaystyle S=\frac{1}{\alpha }+\frac{1}{\beta }=\frac{\alpha +\beta }{\alpha \beta }=\frac{-\frac{b}{a}}{\frac{c}{a}}=-\frac{b}{c} and \displaystyle P=\frac{1}{\alpha }\times \frac{1}{\beta }=\frac{1}{\alpha \beta }=\frac{1}{\frac{c}{a}}=\frac{a}{c}

    Hence, the required polynomial \displaystyle g(x) is given by

        \displaystyle g(x)=k({{x}^{2}}-Sx+P)=k\left( {{x}^{2}}+\frac{bx}{c}+\frac{a}{c} \right), where k is any non-zero constant.

admin