CBSE 10th Mathematics | Similar Triangles | Areas of Similar Triangles

Similar Triangles | Areas of Similar Triangles

Theorem:

The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

Given:
DABC and DPQR such that DABC ~ DPQR.

To prove:
$\displaystyle \frac{\text{ar}\,(\Delta ABC)}{\text{ar}\,(\Delta PQR)}=\frac{A{{B}^{2}}}{P{{Q}^{2}}}=\frac{B{{C}^{2}}}{Q{{R}^{2}}}=\frac{C{{A}^{2}}}{R{{P}^{2}}}$

Construction:
Draw AD ^ BC and PS ^ QR

Proof: $\displaystyle \frac{\text{ar}\,(\Delta ABC)}{\text{ar}\,(\Delta PQR)}=\frac{\frac{1}{2}\times BC\times AD}{\frac{1}{2}\times QR\times PS}$
[ $\displaystyle \because$ Area of triangle $\displaystyle =\frac{1}{2}$ base ´ height]

Þ $\displaystyle \frac{\text{ar}\,(\Delta ABC)}{\text{ar}\,(\Delta PQR)}=\frac{BC}{QR}\times \frac{AD}{PS}$ …(i)

In DADB and DPSQ

ÐB = ÐQ [ $\displaystyle \because$ DABC ~ DPQR]

ÐADB = ÐPSQ [Both 90°]

\ DADB ~ DPSQ [By AA similarity]

Þ $\displaystyle \frac{AD}{PS}=\frac{AB}{PQ}$ …(ii)

[Corresponding sides of similar triangles are proportional]

But $\displaystyle \frac{AB}{PQ}=\frac{BC}{QR}$ [ $\displaystyle \because$ DABC ~ DPQR]

\ $\displaystyle \frac{AD}{PS}=\frac{BC}{QR}$ [Using (ii)] …(iii)

From (i) and (iii), we have

$\displaystyle \frac{\text{ar}\,\,(\Delta ABC)}{\text{ar}\,\,(\Delta PQR)}=\frac{BC}{QR}\times \frac{BC}{QR}=\frac{B{{C}^{2}}}{Q{{R}^{2}}}$ …(iv)

Since DABC ~ DPQR

\ $\displaystyle \frac{AB}{PQ}=\frac{BC}{QR}=\frac{CA}{RP}$ …(v)

Hence, $\displaystyle \frac{\text{ar}\,(\Delta ABC)}{\text{ar}\,(\Delta PQR)}=\frac{A{{B}^{2}}}{P{{Q}^{2}}}=\frac{B{{C}^{2}}}{Q{{R}^{2}}}=\frac{C{{A}^{2}}}{R{{P}^{2}}}$ [From (iv) and (v)]

Solved Questions based on Areas of Similar Triangles

Question:

The areas of two similar triangles ABC and PQR are 64 cm² and 36 cm² respectively. If QR = 16.5 cm, find BC.

Solution:

Since the ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides.

\ $\displaystyle \frac{\text{ar}\,\,(\Delta ABC)}{\text{ar}\,(\Delta PQR)}=\frac{B{{C}^{2}}}{Q{{R}^{2}}}$ Þ $\displaystyle \frac{\text{64}\,\,\text{c}{{\text{m}}^{\text{2}}}}{\text{36}\,\,\text{c}{{\text{m}}^{\text{2}}}}=\frac{B{{C}^{2}}}{{{(16.5\,\,\text{cm})}^{2}}}$

Þ $\displaystyle \frac{8\,\,cm}{6\,\,cm}=\frac{BC}{16.5\,\,cm}$ Þ $\displaystyle BC=\frac{8\times 16.5}{6}\text{cm}=\text{22}\,\,\text{cm}$

Hence BC = 22 cm.

Question:

In the given figure, LM || BC. AM = 3 cm, MC = 4 cm. If the ar(DALM) = 27 cm², calculate the ar(DABC).

Solution:

Given: LM || BC AM = 3 cm, MC = 4 cm and ar(DALM) = 27 cm²

To Find: ar(DABC)

Proof: ÐALM = ÐABC and ÐAML = ÐACB [Corresponding Ðs]

\ DALM ~ DABC [By AA criterion of similarity]

Since the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.

Therefore,

$\displaystyle \frac{\text{ar}\,\,(\Delta ALM)}{\text{ar}\,(\Delta ABC)}=\frac{A{{M}^{2}}}{A{{C}^{2}}}$

Þ $\displaystyle \frac{\text{ar}\,\,(\Delta ALM)}{\text{ar}\,\,(\Delta ABC)}=\frac{A{{M}^{2}}}{{{(AM+MC)}^{2}}}$

Þ $\displaystyle \frac{27\,\text{c}{{\text{m}}^{2}}}{\text{ar}\,\text{(}\Delta ABC\text{)}}=\frac{{{(3\,\,\text{cm)}}^{\text{2}}}}{{{(7\,\text{cm)}}^{\text{2}}}}$

Þ $\displaystyle \text{ar}\,(\Delta ABC)=\left( \frac{27\times 7\times 7}{3\times 3} \right)\,\,\text{c}{{\text{m}}^{2}}$

Þ ar (DABC) = 147 cm²

Question:

D, E, F are the midpoints of the sides BC, CA and AB respectively of DABC. Determine the ratio of the areas of DDEF and DABC.

Solution:

Given: D, E and F are the midpoints of the sides BC,
CA and AB respectively of DABC.

To find:
Ratio of the areas of DDEF and DABC

Proof:
Since D and E are the midpoints of the sides BC and CA respectively of DABC

Therefore, DE || BA
Þ
DE || BF …(i)

Since F and E are the midpoints of AB and AC respectively of DABC.

Therefore, FE || BC
Þ FE || BD …(ii)

From equations (i) and (ii), we get that BDEF is a parallelogram.

\ ÐB = ÐDEF …(iii)

[Opposite angles of a parallelogram BDEF]

Similarly AFDE is a parallelogram

\ ÐA = ÐFDE …(iv)

[Opposite angles of a parallelogram BDEF]

In DABC and DDEF

ÐB = ÐDEF [From (iii)]

ÐA = ÐFDE [From (iv)]

\ DABC ~ DDEF [By AA similarity]

Since the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.

\ $\displaystyle \frac{\text{ar}\,\,(\Delta DEF)}{\text{ar}\,\,(\Delta ABC)}=\frac{D{{E}^{2}}}{A{{B}^{2}}}=\frac{{{\left( \frac{AB}{2} \right)}^{2}}}{A{{B}^{2}}}=\frac{1}{4}$ [ $\displaystyle \because$ By Midpoint Theorem $\displaystyle DE=\frac{1}{2}AB$ ]

Hence, ar(DDEF) : ar(DABC) = 1 : 4

Question:

In figure, the line segment XY is parallel to side AC of DABC and it divides the triangle into two parts of equal areas. Find the ratio 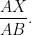$\displaystyle \frac{AX}{AB}.$

Solution:

We have XY || AC [Given]

So, ÐBXY = ÐA and ÐBYX = ÐC [Corresponding angles]

Therefore, DABC ~ DXBY [By AA similarity]

So, $\displaystyle \frac{\text{ar}\,(ABC)}{\text{ar}\,\,(XBY)}={{\left( \frac{AB}{XB} \right)}^{2}}$ …(i)

[The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides]

ar(BXY) = ar(ACYX) [Given]

Adding ar(BXY) to both sides we have

ar(ABC) = 2ar (XBY)

So, $\displaystyle \frac{\text{ar}\,\,(ABC)}{\text{ar}\,\,(XBY)}=\frac{2}{1}$ …(ii)

Therefore, from (i) and (ii),

$\displaystyle {{\left( \frac{AB}{XB} \right)}^{2}}=\frac{2}{1},\,\,i.e.,\,\,\frac{AB}{XB}=\frac{\sqrt{2}}{1}$

or,

$\displaystyle \frac{XB}{AB}=\frac{1}{\sqrt{2}}$

$\displaystyle \frac{AB}{AB}-\frac{AX}{AB}=\frac{1}{\sqrt{2}}$

or,

$\displaystyle 1-\frac{AX}{AB}=\frac{1}{\sqrt{2}}$

or,

$\displaystyle 1-\frac{1}{\sqrt{2}}=\frac{AX}{AB}$

$\displaystyle \frac{\sqrt{2}-1}{\sqrt{2}}=\frac{AX}{AB}$ or $\displaystyle \frac{\sqrt{2}}{\sqrt{2}}\times \frac{\sqrt{2}-1}{\sqrt{2}}$ = $\displaystyle \frac{AX}{AB}$

= $\displaystyle \frac{2-\sqrt{2}}{2}=\frac{AX}{AB}$

Question:

Prove that ratio of areas of two similar triangles is the same as the ratio of the squares of their corresponding medians.

Solution:

Given: Two triangles ABC and PQR such that DABC ~ DPQR

AL and PM are the medians of DABC and DPQR respectively.

To Prove: $\displaystyle \frac{\text{ar}\,(\Delta ABC)}{\text{ar}\,(\Delta PQR)}=\frac{A{{L}^{2}}}{P{{M}^{2}}}$

Proof: DABC ~ DPQR [Given]

Þ $\displaystyle \frac{AB}{PQ}=\frac{BC}{QR}$ [Corresponding sides of similar triangles are proportional]

Þ $\displaystyle \frac{AB}{PQ}=\frac{2BL}{2QM}$ [ $\displaystyle \because$ AL and PM are the medians]

Þ $\displaystyle \frac{AB}{PQ}=\frac{BL}{QM}$ …(i)

Now, in DABL and DPQM, we have

$\displaystyle \frac{AB}{PQ}=\frac{BL}{QM}$ [From (i)]

ÐB = ÐQ [Corr. Ðs of similar triangles]

\ DABL ~ DPQM [By SAS similarity]

Þ $\displaystyle \frac{BL}{QM}=\frac{AL}{PM}$ …(ii)

[Corresponding sides of similar triangles are proportional]

From equation (i) and equation (ii), we have

$\displaystyle \frac{AB}{PQ}=\frac{AL}{PM}\Rightarrow \frac{A{{B}^{2}}}{P{{Q}^{2}}}=\frac{A{{L}^{2}}}{P{{M}^{2}}}$ …(iii)

Since the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

Therefore, $\displaystyle \frac{\text{ar}\,(\Delta ABC)}{\text{ar}\,\text{(}\Delta PQR\text{)}}=\frac{A{{B}^{2}}}{P{{Q}^{2}}}$ …(iv)

From equation (iii) and equation (iv), we have

$\displaystyle \frac{\text{ar}\,\,(\Delta ABC)}{\text{ar}\,\text{(}\Delta PQR\text{)}}=\frac{A{{L}^{2}}}{P{{M}^{2}}}$

Question:

Prove that the area of the equilateral triangle BCE described on one side BC of a square ABCD as base is half the area of the equilateral triangle ACF described on the diagonal AC as base.

Solution:

Given:
ABCD is a square. DBCE is described on side BC is similar to DACF described on diagonal AC.

To Prove:
ar(DCBE) = $\displaystyle \frac{1}{2}$ ar(DACF)

Proof:
ABCD is a square. Therefore,

$\displaystyle AB=BC=CD=DA$ and, $\displaystyle AC=\sqrt{2}BC$ [ $\displaystyle \because$ Diagonal = $\displaystyle \sqrt{2}$ (Side)]

Now, $\displaystyle \Delta$ BCE ~ DACF [Both are equiangular hence similar by AA criteria]

Þ $\displaystyle \frac{\text{Area}\,(\Delta BCE)}{\text{Area}\,(\Delta ACF)}=\frac{B{{C}^{2}}}{A{{C}^{2}}}$

Þ $\displaystyle \frac{\text{Area}\,(\Delta BCE)}{\text{Area}\,\,(\Delta ACF)}=\frac{B{{C}^{2}}}{{{(\sqrt{2}BC)}^{2}}}=\frac{1}{2}$

Þ $\displaystyle \text{Area}\,(\Delta BCE)=\frac{1}{2}\text{Area}\,(\Delta ACF)$

Question:

In figure, DE || BC and AD : DB = 5 : 4. Find $\displaystyle \frac{\text{Area}\,(\Delta DEF)}{\text{Area}\,\,(\Delta CFB)}.$

Solution:

Given:
DE || BC and AD : DB = 5 : 4

To find: $\displaystyle \frac{\text{Area}\,(\Delta DEF)}{\text{Area}\,\,(\Delta CFB)}.$

Proof: In DABC,

Since DE || BC [Given]

Þ ÐADE = ÐABC and ÐAED = ÐACB [Corresponding angles]

In triangles ADE and ABC, we have

ÐA = ÐA [Common]

ÐADE = ÐABC [Proved above]

and, ÐAED = ÐACB [Proved above]

\ DADE ~ DABC [By AAA similarity]

Þ $\displaystyle \frac{AD}{AB}=\frac{DE}{BC}$

We have,

$\displaystyle \frac{AD}{DB}=\frac{5}{4}$

Þ $\displaystyle \frac{DB}{AD}=\frac{4}{5}$

Þ $\displaystyle \frac{DB}{AD}+1=\frac{4}{5}+1$ [Adding 1 to both sides]

Þ $\displaystyle \frac{DB+AD}{AD}=\frac{9}{5}$

Þ $\displaystyle \frac{AB}{AD}=\frac{9}{5}$

\ $\displaystyle \frac{DE}{BC}=\frac{5}{9}$ …(i)

In DDEF and DCFB, we have

Ð1 = Ð3 [Alternate interior angles]

Ð2 = Ð4 [Vertically opposite angles]

\ DDFE ~ DCFB [By AA similarity]

Þ $\displaystyle \frac{\text{Area}\,\,(\Delta \,DFE)}{\text{Area}\,(\Delta CFB)}=\frac{D{{E}^{2}}}{B{{C}^{2}}}$

Þ $\displaystyle \frac{\text{Area}\,(\Delta DFE)}{\text{Area}\,(\Delta CFB)}={{\left( \frac{5}{9} \right)}^{2}}=\frac{25}{81}$ [From (i)]

Question:

In the given figure, ABCD is a trapezium in which AB || DC and AB = 2 CD. Find the ratio of the areas of triangles AOB and COD.

Solution:

Given: ABCD is a trapezium in which AB || DC and AB = 2 CD

To Find: Ratio of the areas of triangles AOB and COD

Proof: In DAOB and DCOD,

ÐAOB = ÐCOD [Vertically opposite angles]

ÐOAB = ÐOCD [Alternate angles as AB || DC]

\ DAOB ~ DCOD [By AA similarity]

Since the ratio of the areas of two similar triangles is equal to the ratio of squares of any two corresponding sides

\ $\displaystyle \frac{\text{ar}\,(\Delta AOB)}{\text{ar}\,(\Delta COD)}=\frac{A{{B}^{2}}}{C{{D}^{2}}}=\frac{{{(2\,CD)}^{2}}}{C{{D}^{2}}}$ [ $\displaystyle \because$ AB = 2 CD]

$\displaystyle =\frac{4\,C{{D}^{2}}}{C{{D}^{2}}}=\frac{4}{1}$

Hence, ar(AOB) : ar(DCOD) = 4 : 1

Question:

In figure, prove that $\displaystyle \frac{\text{Area}\,(\Delta ABC)}{\text{Area}\,(\Delta DBC)}=\frac{AO}{DO}.$

Solution:

Construction: Draw AX and DY ^ BC

Proof:
In DAOX and DDOY, we have

ÐAXO = ÐDYO [Both 90°]

ÐAOX = ÐDOY [Vert. Opp. angles]

\ DAOX ~ DDOY [By AA similarity]

Þ $\displaystyle \frac{AX}{DY}=\frac{AO}{DO}$ …(i)

Now $\displaystyle \frac{\text{Area}\,(\Delta ABC)}{\text{Area}\,\text{(}\Delta DBC\text{)}}=\frac{\frac{1}{2}BC\times AX}{\frac{1}{2}BC\times DY}=\frac{AX}{DY}$

Thus, $\displaystyle \frac{Area\,(\Delta ABC)}{Area\,(\Delta DBC)}=\frac{AO}{DO}$ [Using (i)]

Question:

Two isosceles triangles have equal vertical angles and their area are in the ratio 16 : 25. Find the ratio of their corresponding heights.

Solution:

Given:
Let DABC and DDEF be the given triangles such that AB = AC and DE = DF, ÐA = ÐD

and, $\displaystyle \frac{\text{Area}\,(\Delta ABC)}{\text{Area}\,(\Delta DEF)}=\frac{16}{25}$ …(i)

To Find : $\displaystyle \frac{AL}{DM}$

Construction: Draw AL ^ BC and DM ^ EF

Proof: Now, AB = AC, DE = DF

Þ $\displaystyle \frac{AB}{AC}=1$ and $\displaystyle \frac{DE}{DF}=1$

Þ $\displaystyle \frac{AB}{AC}=\frac{DE}{DF}$

Þ $\displaystyle \frac{AB}{DE}=\frac{AC}{DF}$

Thus, in triangles ABC and DEF, we have

$\displaystyle \frac{AB}{DE}=\frac{AC}{DF}$ and ÐA = ÐD [Given]

So, by SAS-similarity criterion, we have

DABC ~ DDEF

Þ $\displaystyle \frac{Area\,(\Delta ABC)}{Area\,(\Delta DEF)}=\frac{A{{L}^{2}}}{D{{M}^{2}}}$ [Ratio of areas of two similar triangles is equal to ratio of squares of their corresponding altitudes]

Þ $\displaystyle \frac{16}{25}=\frac{A{{L}^{2}}}{D{{M}^{2}}}$ [Using (i)]

Þ $\displaystyle \frac{4}{5}=\frac{AL}{DM}$

CBSE Tutorials

CBSE 10th Mathematics | Similar Triangles | Areas of Similar Triangles

Similar Triangles | Areas of Similar Triangles

Solved Questions based on Areas of Similar Triangles

Question:

The areas of two similar triangles ABC and PQR are 64 cm² and 36 cm² respectively. If QR = 16.5 cm, find BC.

Solution:

Question:

In the given figure, LM || BC. AM = 3 cm, MC = 4 cm. If the ar(DALM) = 27 cm², calculate the ar(DABC).

Solution:

Question:

D, E, F are the midpoints of the sides BC, CA and AB respectively of DABC. Determine the ratio of the areas of DDEF and DABC.

Solution:

Question:

In figure, the line segment XY is parallel to side AC of DABC and it divides the triangle into two parts of equal areas. Find the ratio $\displaystyle \frac{AX}{AB}.$

Solution:

Question:

Prove that ratio of areas of two similar triangles is the same as the ratio of the squares of their corresponding medians.

Solution:

Question:

Prove that the area of the equilateral triangle BCE described on one side BC of a square ABCD as base is half the area of the equilateral triangle ACF described on the diagonal AC as base.

Solution:

Question:

In figure, DE || BC and AD : DB = 5 : 4. Find $\displaystyle \frac{\text{Area}\,(\Delta DEF)}{\text{Area}\,\,(\Delta CFB)}.$

Solution:

Question:

In the given figure, ABCD is a trapezium in which AB || DC and AB = 2 CD. Find the ratio of the areas of triangles AOB and COD.

Solution:

Question:

In figure, prove that $\displaystyle \frac{\text{Area}\,(\Delta ABC)}{\text{Area}\,(\Delta DBC)}=\frac{AO}{DO}.$

Solution:

Question:

Two isosceles triangles have equal vertical angles and their area are in the ratio 16 : 25. Find the ratio of their corresponding heights.

Solution:

Like this:

CBSE 10th Mathematics | Similar Triangles | Areas of Similar Triangles

Similar Triangles | Areas of Similar Triangles

Solved Questions based on Areas of Similar Triangles

Question:

The areas of two similar triangles ABC and PQR are 64 cm2 and 36 cm2 respectively. If QR = 16.5 cm, find BC.

Solution:

Question:

In the given figure, LM || BC. AM = 3 cm, MC = 4 cm. If the ar(DALM) = 27 cm2, calculate the ar(DABC).

Solution:

Question:

D, E, F are the midpoints of the sides BC, CA and AB respectively of DABC. Determine the ratio of the areas of DDEF and DABC.

Solution:

Question:

In figure, the line segment XY is parallel to side AC of DABC and it divides the triangle into two parts of equal areas. Find the ratio

Solution:

Question:

Prove that ratio of areas of two similar triangles is the same as the ratio of the squares of their corresponding medians.

Solution:

Question:

Prove that the area of the equilateral triangle BCE described on one side BC of a square ABCD as base is half the area of the equilateral triangle ACF described on the diagonal AC as base.

Solution:

Question:

In figure, DE || BC and AD : DB = 5 : 4. Find

Solution:

Question:

In the given figure, ABCD is a trapezium in which AB || DC and AB = 2 CD. Find the ratio of the areas of triangles AOB and COD.

Solution:

Question:

In figure, prove that

Solution:

Question:

Two isosceles triangles have equal vertical angles and their area are in the ratio 16 : 25. Find the ratio of their corresponding heights.

Solution:

Share this:

Like this:

The areas of two similar triangles ABC and PQR are 64 cm² and 36 cm² respectively. If QR = 16.5 cm, find BC.

In the given figure, LM || BC. AM = 3 cm, MC = 4 cm. If the ar(DALM) = 27 cm², calculate the ar(DABC).

In figure, the line segment XY is parallel to side AC of DABC and it divides the triangle into two parts of equal areas. Find the ratio $\displaystyle \frac{AX}{AB}.$

In figure, DE || BC and AD : DB = 5 : 4. Find $\displaystyle \frac{\text{Area}\,(\Delta DEF)}{\text{Area}\,\,(\Delta CFB)}.$

In figure, prove that $\displaystyle \frac{\text{Area}\,(\Delta ABC)}{\text{Area}\,(\Delta DBC)}=\frac{AO}{DO}.$