Force and Laws of Motion: Part 3

Law of Conservation of momentum: –

According to this law, the total momentum of an object remains constant if no net external force is applied on the object.

Illustration of the law of conservation of momentum: –

Let a moving ball collides with a stationary ball lying on the ground, observe what happens after collision. The moving ball will slow down i.e. its velocity decreases after colliding with the stationary ball.

On the other hand, the stationary ball beings to move i.e. its velocity increase after collision. We know, momentum of a body = mass of the body velocity of the body

Therefore, the momentum of moving ball decrease after collision and the momentum of the stationary ball increase after collision.

Thus, we find that when two balls collide with each other, then moving ball loses momentum and the stationary ball gains momentum. The loss of momentum of one ball is equal to the gain of momentum of other ball.

However, the total momentum of these colliding balls before and after the collision remains the same. This is the law of conservation of momentum.

Proof of the law of conservation of momentum: –

Consider a system consisting of two bodies A and B of masses m₁ and m₂ respectively. suppose these bodies are moving with velocities u₁and u₂ as shown in fig below Let u₁ > u₂

These bodies collide with each other for a small interval of time t. At the time of collision F_AB is the force on A due to B and F_BA is the force on B due to A. According to Newton’s third law of motion F_AB = – F_BA.

Due to these forces, the momentum of the bodies changes. Let V₁ and V₂ is the velocities of body

A and body B respectively after collision.

Now, initial momentum of body A = m₁u₁

Initial momentum of body B = m₂u₂

Final momentum of body A = m₁v₁

Final momentum of body B = m₂ v₂

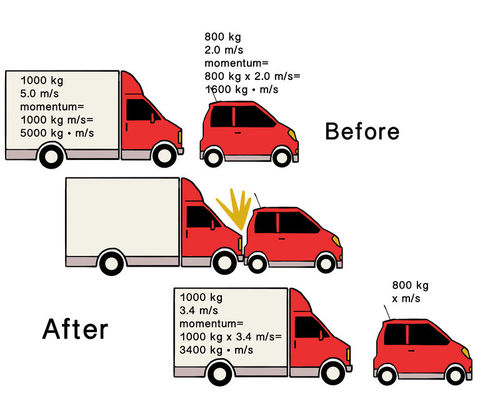
Total momentum of the system before collision = m₁ u₁ + m₂ u₂

Total momentum of the system after collision = m₁v₁ + m₂ v₂

Change in momentum of the body A = final momentum of body A – Initial momentum of body A

= m₁v₁ – m₁u₁

and change in momentum of the body B = final momentum of body B – initial momentum of body B

= m₂ v₂ – m₂ u₂

According to Newton’s second law of motion

and

According to Newton’s third law of motion F_AB = –F _BA

or

or

or

or

Hence, total momentum of the system before collision = Total momentum of the system after collision.

This is the law of conservation of momentum.

Application of conservation of Momentum

(i) Rocket Propulsion (Movement of A rocket in the upward direction)

The movement of a rocket in the upward direction can also be explained with the help of the law of conservation of momentum.

The momentum of rocket before it is fired is zero. When the rocket is fired, gases are produced in the combustion chamber of the rocket due to the burning of fuel. These gases come out of the rear of the rocket with high speed. The direction of the momentum of the gases coming out of the rocket is in the downward direction. To conserve the momentum of the system (rocket + gases), the rocket moves upward with a momentum equal to the momentum of gases. The rockets continue to move upward as long as the gases are ejected out of the rocket.

(ii) Inflated balloon lying on the surface of a floor moves forward when pierced with a pin: –

The momentum of the inflated balloon before it is pierced wit a pin is zero. When it is pierced with a pin, air in it comes out with in the backward direction. To conserve the momentum, the balloon moves in the forward direction.

(iii) Recoil of gun:

The recoil of a gun can also be explained with the help of the law of conservation of momentum. Before firing, the gun and the bullet are at rest, therefore, momentum of the system before firing is zero.

When the bullet is fired, it leaves the gun in the forward direction with certain momentum. Since no external force acts on the system, so the momentum of the system must be zero after firing. This is possible only if the gun moves backward with a momentum equal to the momentum of the bullet. That is why gun recoils or moves backward.

Recoil velocity of a gun

Let, mass of the bullet = m

Velocity of the bullet after firing = v

Mass of the gun = M.

Velocity of the gun after firing = V

Since the system is at rest before firing, so moment of the system (gun + bullet) before firing = 0

According to the law of conservation of momentum,

Momentum of system after firing = Moment of system before firing

i.e. MV + mv = 0

or, MV = – mv

or,

Negative sign shows that the direction of the velocity of the gun after firing is opposite to the direction of the velocity of the bullet.