CBSE Tutorials

Physics 9th: Motion | Derivation of Equations of Motion by Graphical Method

Physics 9th: Motion | Derivation of Equations of Motion by Graphical Method

Derivation of Equations of Motion by Graphical Method

 

TO DERIVE v = u + at BY GRAPHICAL METHOD

 

This is a graph of uniform acceleration with ‘u’ as initial velocity and ‘v’ as final velocity.

    Initial velocity = u = OP

    Final velocity = v = RN

             = RQ + QN

             v = u + QN    …..(i)

    Acceleration, a = slope of line PN

         \displaystyle a=\frac{QN}{PQ}=\frac{QN}{t}

         \displaystyle QN=at        …..(ii)

    Putting the value of QN from equation (ii) into equation (i), we get v = u + at        

 

TO DERIVE \displaystyle s=ut+\frac{1}{2}a{{t}^{2}} BY GRAPHICAL METHOD

 

    In the above speed-time graph, the distance travelled is given by

            Distance travelled = Area of figure OPNR

                     = Area of DPNQ + Area of rectangle OPQR

    (1)     Area of triangle PNQ = \displaystyle \frac{1}{2}\times base\times height

                     = \displaystyle \frac{1}{2}\times PQ\times NQ \displaystyle =\frac{1}{2}\times t\times (v-u)

                     = \displaystyle \frac{1}{2}\times t\times at    [As v = u + at and v – u = at]

             Area of DPNQ = \displaystyle \frac{1}{2}a{{t}^{2}}

    (2)    Area of rectangle OPQR = OP ´ PQ

                      = u ´ t

                      = ut    

    Distance travelled = Area of DPNQ + Area of rectangle OPQR

    \displaystyle S=\frac{1}{2}a{{t}^{2}}+ut

    \displaystyle S=ut+\frac{1}{2}a{{t}^{2}}

TO DERIVE 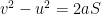\displaystyle {{v}^{2}}-{{u}^{2}}=2aS BY GRAPHICAL METHOD

 

    In the above speed time graph distance travelled (S) = Area of trapezium OPNR

    \displaystyle S=\frac{1}{2}\times (sum of parallel sides) ´ height

    \displaystyle S=\frac{1}{2}\times (OP + RN) ´ OR

    \displaystyle S=\frac{1}{2}\times (u + v) ´ t

    \displaystyle S=\frac{1}{2}\times (v + u) t            …(i)

    But v = u + at

    at = v – u

    \displaystyle t=\left( \frac{v-u}{a} \right)                … (ii)

    Putting this value of ‘t’ from equation (ii) into equation (i) we get that ___

    \displaystyle S=\frac{1}{2}\times (v + u) \displaystyle \left( \frac{v-u}{a} \right)

    \displaystyle S=\frac{\left( v+u \right)\left( v-u \right)}{2a}

    \displaystyle S=\frac{{{v}^{2}}-{{u}^{2}}}{2a}        [As (a + b) (a – b) = \displaystyle {{a}^{2}}-{{b}^{2}}]

    2as = \displaystyle {{v}^{2}}-{{u}^{2}}

    \displaystyle {{v}^{2}}-{{u}^{2}}=2as

        

admin